الانماط الطبيعية Normal Modes

(i)......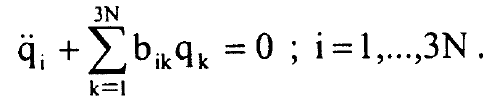

يمكن تبسيط المعادلة (i) باستخدام المتجهات {q = {q₁, ....,q_3N لتصبح بالشكل:

........(1)

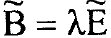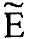حيث مصفوفة بالمركبات (b_ik) واذا كانت مصفوفة قطرية خاصة  ( مصفوفة الوحدة) فان المعادلة (1) ستختزل الى نظام من المعادلات الاهتزازية المستقلة عددا 3N للاحداثي q_i وحلولها تعطى بالمعادلة:

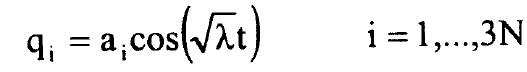...........(2)

وتصف الحلول (2) حالة جزيئية تهتز كل النوى فيها بنفس التردد وتمر من مواقع اتزانها آنيا ولذلك نحتاج نظام احداثيات اهتزازية يجعل قطرية.

ان الشرط:

...........(3)

يساوي تحويل المحور الاساسي ويملك حلولا غير بديهية اذا كان:

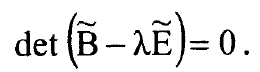..........(4)

ولكل حل λ_n للمعادلة (4) نحصل من المعادلة (3) على مجموعة 3N مركبة اهتزازية q_kn (k = 1,….,3N)ويمكن جمع q_kn في المتجه:

...........(5)

ويصف المتجه في المعادلة (5) الحركة الآنية لكل النوى خلال الاهتزاز الطبيعي n ويدعى مقدار المتجه Q_n الاحداثي الطبيعي للنمط الطبيعي بالتردد 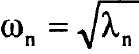لذا فان الاحداثي الطبيعي Q_n(t) يعطي ازاحات كل النوى عند اللحظة t خلال الاهتزاز الطبيعي n.

وباستخدام الاحداثيات الطبيعية يمكن كتابة المعادلة (1) كمجموعة معادلات مستقلة عددها 3N:

..........(6)

ولان كلا من الطاقة الحركية والطاقة الكامنة في الشكل التربيعي بعد اهمال حدود المرتبة الاعلى في الطاقة الكامنة تعطى بالصيغة:

............(7)

فان حلول المعادلة (6) تكون الاهتزازات الطبيعية في المعادلة (5).

يتبين مما سبق ان الجزيئة تهتز بحركة توافقية بالاحداثيات الطبيعية لسعة الاهتزاز القليلة بالتردد نفسه لكل النوى وبنفس او عكس الطور φ_i الاهتزاز الطبيعي معطى I والطاقة الاهتزازية الكلية للجزيئة تساوي جمع الطاقات الاهتزازية لكل الاهتزازات الطبيعية المتهيجة.

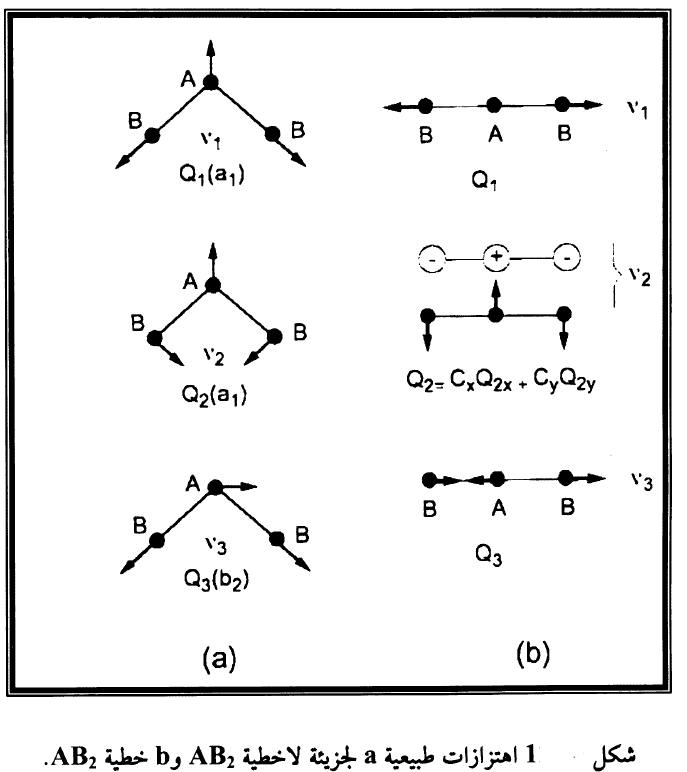
ان الطاقة الكامنة V تعتمد على الاحداثيات الداخلية فقط (المسافات بين النوى والالكترونات) وليس على انتقال ودوران الاطار النووي لذلك فان بعض المكافئات b_ik في المعادلة (i) يجب ان تتلاشى وبعد السماح لثلاث درجات حرية انتقالية ومثلها دورانية تبقى (3N-6) درجة حرية لاهتزاز جزيئة لاخطية و(3N-5) درجة حرية لجزيئة خطية لان الجزيئات الخطية لا تدور حول المحور الواصل بين النوى لذا يوجد (3N-6) حل غير متلاشي λ_n لجزيئة لا خطية و(3N-5) حل لجزيئة خطية وفي شكل 4-12 مبين اهتزازات طبيعية لجزيئة خطية AB₂ ولا خطية AB₂.

اخر الاخبار

اخبار العتبة العباسية المقدسة

أهالي كربلاء يحيون اليوم السابع لذكرى شهادة الإمام الحسين (عليه السلام)

مشروع أمير القراء الوطني يشهد مشاركة أكثر من 100 طالبٍ في مرحلته الثالثة

قسم الشؤون الفكرية يصدر دليلًا يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة

قسم الشؤون الفكرية يعلن عن توفير عددٍ من المكتبات الإلكترونية المتخصّصة للمؤسّسات الدينية والمكتبات العامّة

المزيد

الآخبار الصحية

نصائح عملية للحد من التعرق المفرط في الصيف

أطباء يحذرون: مكمل غذائي شائع قد يدمر الجهاز العصبي

تحذير طبي من تأثير جانبي "غير متوقع" لحقن التخسيس

حمامات الثلج قد تكون خطيرة وأحيانا مميتة.. ما السبب؟

المزيد

الآخبار التكنلوجية

أكبر جدارية شمسية في العالم تدخل موسوعة غينيس.. مشروع ضخم

تسارع دوران الأرض يثير القلق.. وتحذيرات من "كوارث محتملة" ؟

"سوذبيز" تطرح أكبر قطعة من المريخ على الأرض في مزاد علني

أوبن أيه آي تعتزم إطلاق متصفح إنترنت يعمل بالذكاء الاصطناعي

المزيد

مواضيع ذات صلة

الكشف عن الألغام والمتفجرات

الكربون .. أمير المواد وعميدها

خواص المواد النانوية

تاريخ أنابيب الكربون النانوية (History of carbon nanotubes)

الاتصال والحوار العام في تطوير تقنية النانو

نشاطات المنظمات الدولية في مجال التقنية النانوية

حالة المعارف المتصلة بمخاطر المواد النانوية

الاعتبارات الأخلاقية في التقنية النانويه

المنفعة الاجتماعية للتقنية النانوية

ما المقصود بالنانو؟

النانو تكنولوجيا.. علم وصناعة القرن الجديد

أنابيب الكربون النانوية Nanotubes Carbon