The rascal triangle is a number triangle with numbers arranged in staggered rows such that

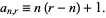(1)

The published study of this triangle seems to have originated relatively recently, having been added to Sloane's Online Encyclopedia of Integer Sequences (OEIS) as recently as 2002--where it was cataloged as [t]riangle with diagonal  congruent to  mod --and having been the subject of scholarly mathematical publication as recently as 2010 (Anggoro et al. 2010). The triangle is sometimes written without capitalization as the rascal triangle.

One common point of exposition among literature regarding the rascal triangle is its similarity to Pascal's triangle. Indeed, the rascal triangle is topically similar to Pascal's triangle in that the configuration starting with 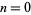 begins

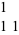(2)

and that the rows afterwards have their first and last entries equal to

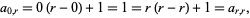(3)

respectively.

The similarities don't end there, however. One well-known fact about Pascal's triangle is that the interior entries of each row are determined by the so-called inverted triangle formula

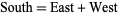(4)

as shown in the diagram above.

On the other hand, the rows of the rascal triangle have interior entries which are determined by a so-called diamond formula of the form

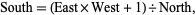(5)

whereby one can compute the first few rows of the rascal triangle to have the form

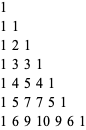(6)

(OEIS A077028). Surprisingly, each interior entry of the rascal triangle remains integer-valued despite the fact that, as shown in (), every such entry is computed using integer division (Anggoro et al. 2010).

By examining the first few rows of the rascal triangle, one can hypothesize the validity of a number of significant number-theoretic properties thereof. For example, the values given support the claim (OEIS A077028) that each element of the 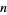th diagonal is congruent to 1 modulo 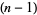, e.g., in the fourth diagonal, where each of

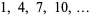(7)

is congruent to 1 modulo 3. Here, 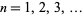. Moreover, one notices that the 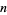th number on the 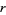th row  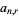appears to be--and is--precisely the 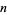th number on the 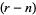th diagonal (Anggoro et al. 2010) where, here,  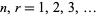and the 0th row is excluded. This observation is fundamental in proving that the rascal triangle consists strictly of integers.

There are a number of other colorful properties of the rascal triangle. For example, the sums of the rows of the rascal triangle are the so-called cake numbers (OEIS A000125):

			(8)
			(9)
			(10)
			(11)
			(12)
			(13)

Several other authors have noted interesting connections between numbers in the rascal triangle and various other fields of mathematics including group theory, linear algebra, and geometric analysis.

REFERENCES:

Anggoro, A.; Liu, E.; and Tulloch, A. "The Rascal Triangle." College Math. J. 41, 393-395, 2010.

Bogomolny, A. "The Rascal Triangle." Interactive Mathematics Miscellany and Puzzles. https://www.cut-the-knot.org/arithmetic/algebra/RascalTriangle.shtml.

Sloane, N. J. A. Sequences A077028, A007318, A000125, and A128139 in "The On-Line Encyclopedia of Integer Sequences."

اخر الاخبار

اخبار العتبة العباسية المقدسة

مستشفى الكفيل يعلن انضمامه لمشروع الضمان الصحي الحكومي

المجمَع العلمي يقيم مسابقة الكوثر الخاصة بترتيل القرآن الكريم في كربلاء

قسم الشؤون الفكرية والثقافية يُصدر العدد الثالث والعشرين من مجلّة (أوراق معرفية)

قسم التربية والتعليم يُطلق الموسم التدريبيّ الصيفيّ لملاكات مجموعة العميد التربوية

المزيد

الآخبار الصحية

اختراق علمي.. دواء يؤخر ظهور السكري من النوع الأول لسنوات

هذا ما يحدث لجسمك إن أهملت نظافة فراشك

لماذا تعتبر النساء أكثر عرضة للإصابة بألزهايمر من الرجال؟

لماذا يحذر الخبراء من الإفراط في تناول الفراولة؟

المزيد

الآخبار التكنلوجية

السيارات الكهربائية أنظف بنسبة 73% من سيارات الوقود

سيارة لوسِد الكهربائية تدخل "غينيس" بأطول مدى في العالم

نظرية جديدة تنسف كل ما نعرفه عن تشكل أول قارة في الأرض

منذ 37 ألف عام.. دراسة تكشف "أقدم أمراض" أصابت البشر

المزيد