Sárkőzy's Theorem

A partial solution to the Erdős squarefree conjecture which states that the binomial coefficient 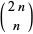 is never squarefree for all sufficiently large 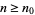. Sárkőzy (1985) showed that if  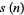is the square part of the binomial coefficient 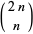, then

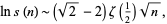where 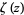 is the Riemann zeta function. An upper bound on  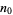of 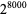 has been obtained.

REFERENCES:

Erdős, P. and Graham, R. L. Old and New Problems and Results in Combinatorial Number Theory. Geneva, Switzerland: L'Enseignement Mathématique Université de Genève, Vol. 28, 1980.

Sander, J. W. "A Story of Binomial Coefficients and Primes." Amer. Math. Monthly 102, 802-807, 1995.

Sárkőzy, A. "On the Divisors of Binomial Coefficients, I." J. Number Th. 20, 70-80, 1985.

Vardi, I. "Applications to Binomial Coefficients." Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 25-28, 1991.