


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-10-2020
Date: 16-12-2020
Date: 26-6-2020
|
A sequence of numbers 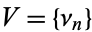 is complete if every positive integer
is complete if every positive integer 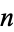 is the sum of some subsequence of
is the sum of some subsequence of 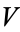 , i.e., there exist
, i.e., there exist 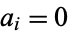 or 1 such that
or 1 such that
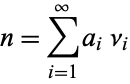 |
(Honsberger 1985, pp. 123-126). The Fibonacci numbers are complete. In fact, dropping one number still leaves a complete sequence, although dropping two numbers does not (Honsberger 1985, pp. 123 and 126). The sequence of primes with the element 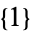 prepended,
prepended,
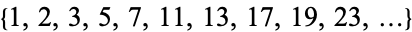 |
is complete, even if any number of primes each 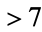 are dropped, as long as the dropped terms do not include two consecutive primes (Honsberger 1985, pp. 127-128). This is a consequence of Bertrand's postulate.
are dropped, as long as the dropped terms do not include two consecutive primes (Honsberger 1985, pp. 127-128). This is a consequence of Bertrand's postulate.
REFERENCES:
Brown, J. L. Jr. "Unique Representations of Integers as Sums of Distinct Lucas Numbers." Fib. Quart. 7, 243-252, 1969.
Hoggatt, V. E. Jr.; Cox, N.; and Bicknell, M. "A Primer for Fibonacci Numbers. XII." Fib. Quart. 11, 317-331, 1973.
Honsberger, R. Mathematical Gems III. Washington, DC: Math. Assoc. Amer., 1985.



|
|
|
|
حقن الذهب في العين.. تقنية جديدة للحفاظ على البصر ؟!
|
|
|
|
|
|
|
علي بابا تطلق نماذج "Qwen" الجديدة في أحدث اختراق صيني لمجال الذكاء الاصطناعي مفتوح المصدر
|
|
|
|
|
|
|
ضمن برنامج تأهيل المنتسبين الجدد قسم الشؤون الدينية يقدم محاضرات فقهية وعقائدية لنحو 130 منتسبًا
|
|
|