

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Landau-Ramanujan Constant
المؤلف:
Berndt, B. C
المصدر:
Ramanujan,s Notebooks, Part IV. New York: Springer-Verlag
الجزء والصفحة:
...
27-12-2020
1292
Landau-Ramanujan Constant
Let 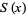 denote the number of positive integers not exceeding
denote the number of positive integers not exceeding  which can be expressed as a sum of two squares (i.e., those
which can be expressed as a sum of two squares (i.e., those 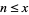 such that the sum of squares function
such that the sum of squares function 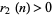 ). For example, the first few positive integers that can be expressed as a sum of squares are
). For example, the first few positive integers that can be expressed as a sum of squares are
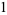 |
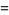 |
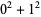 |
(1) |
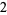 |
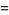 |
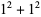 |
(2) |
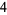 |
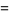 |
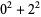 |
(3) |
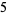 |
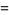 |
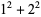 |
(4) |
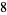 |
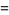 |
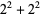 |
(5) |
(OEIS A001481), so 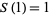 ,
, 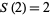 ,
, 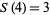 ,
, 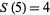 ,
, 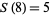 , and so on. Then
, and so on. Then
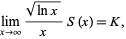 |
(6) |
as proved by Landau (1908), where 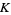 is a constant. Ramanujan independently stated the theorem in the slightly different form that the number of numbers between
is a constant. Ramanujan independently stated the theorem in the slightly different form that the number of numbers between 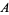 and
and  which are either squares of sums of two squares is
which are either squares of sums of two squares is
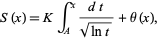 |
(7) |
where 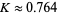 and
and 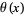 is very small compared with the previous integral (Berndt and Rankin 1995, p. 24; Hardy 1999, p. 8; Moree and Cazaran 1999).
is very small compared with the previous integral (Berndt and Rankin 1995, p. 24; Hardy 1999, p. 8; Moree and Cazaran 1999).
Note that for 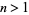 ,
, 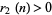 iff
iff 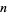 is not divisible by a prime power
is not divisible by a prime power 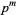 with
with 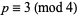 and
and 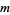 odd.
odd.
The constant has numerical value
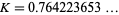 |
(8) |
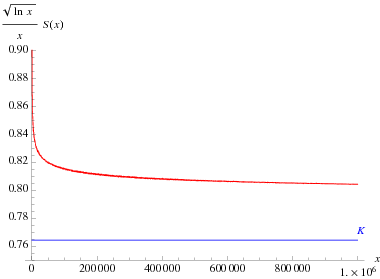
(OEIS A064533). However, the convergence to the constant 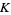 , known as the Landau-Ramanujan constant and sometimes also denoted
, known as the Landau-Ramanujan constant and sometimes also denoted 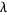 , is very slow. The following table summarizes the values of the left side of equation (7) for the first few powers of 10, where the sequence of
, is very slow. The following table summarizes the values of the left side of equation (7) for the first few powers of 10, where the sequence of 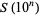 is (OEIS A164775).
is (OEIS A164775).
 |
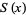 |
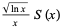 |
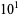 |
7 | 1.062199 |
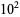 |
43 | 0.922765 |
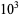 |
330 | 0.867326 |
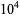 |
2749 | 0.834281 |
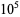 |
24028 | 0.815287 |
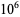 |
216341 | 0.804123 |
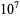 |
1985459 | 0.797109 |
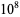 |
18457847 | 0.792198 |
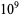 |
173229058 | 0.788587 |
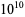 |
1637624156 | 0.785818 |
An exact formula for the constant is given by
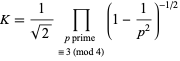 |
(9) |
(Landau 1908; Le Lionnais 1983, p. 31; Berndt 1994; Hardy 1999; Moree and Cazaran 1999), and an equivalent formula is given by
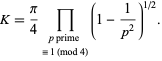 |
(10) |
Flajolet and Vardi (1996) give a beautiful formula with fast convergence
![K=1/(sqrt(2))product_(n=1)^infty[(1-1/(2^(2^n)))(zeta(2^n))/(beta(2^n))]^(1/2^(n+1)),](https://mathworld.wolfram.com/images/equations/Landau-RamanujanConstant/NumberedEquation6.gif) |
(11) |
where 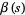 is the Dirichlet beta function.
is the Dirichlet beta function.
Another closed form is
![K=lim_(n->infty)(sqrt(lnn))/nsum_(k=1)^n[1-delta_(0,r_2(k))],](https://mathworld.wolfram.com/images/equations/Landau-RamanujanConstant/NumberedEquation7.gif) |
(12) |
where 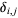 is the Kronecker delta and
is the Kronecker delta and 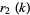 is the sum of squares Function.
is the sum of squares Function.
W. Gosper used the related formula
![K=1/2[1/(Psi(2)-1)]^(sqrt(2))product_(k=2)^infty[1/(-Psi(2^k)-1)]^(1/(2^(k+1))),](https://mathworld.wolfram.com/images/equations/Landau-RamanujanConstant/NumberedEquation8.gif) |
(13) |
where
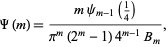 |
(14) |
where 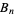 is a Bernoulli number and
is a Bernoulli number and 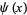 is a polygamma function (Finch 2003).
is a polygamma function (Finch 2003).
Landau also proved the even stronger fact
![lim_(x->infty)((lnx)^(3/2))/(Kx)[S(x)-(Kx)/(sqrt(lnx))]=C,](https://mathworld.wolfram.com/images/equations/Landau-RamanujanConstant/NumberedEquation10.gif) |
(15) |
where
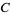 |
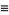 |
![1/2[1-ln((pie^gamma)/(2L))]-1/4d/(ds)[ln(product_(p prime; = 3 (mod 4))1/(1-p^(-2s)))]_(s=1)](https://mathworld.wolfram.com/images/equations/Landau-RamanujanConstant/Inline59.gif) |
(16) |
 |
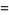 |
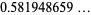 |
(17) |
(OEIS A085990), e is the base of the natural logarithm, 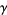 is the Euler-Mascheroni constant, and
is the Euler-Mascheroni constant, and 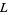 is the lemniscate constant.
is the lemniscate constant.
Landau's method of proof can be extended to show that
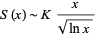 |
(18) |
has an asymptotic series
![S(x)=Kx/(sqrt(lnx))[1+(c_1)/(lnx)+(c_2)/((lnx)^2)+...+(c_n)/((lnx)^n)+O(1/((lnx)^(n+1)))],](https://mathworld.wolfram.com/images/equations/Landau-RamanujanConstant/NumberedEquation12.gif) |
(19) |
where 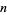 can be arbitrarily large and the
can be arbitrarily large and the 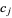 are constants with
are constants with 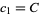 (Moree and Cazaran 1999).
(Moree and Cazaran 1999).
REFERENCES:
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 60-66, 1994.
Berndt, B. C. and Rankin, R. A. Ramanujan: Letters and Commentary. Providence, RI: Amer. Math. Soc., pp. 25, 47, and 49, 1995.
Finch, S. R. "Landau-Ramanujan Constant." §2.3 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 98-104, 2003.
Flajolet, P. and Vardi, I. "Zeta Function Expansions of Classical Constants." Unpublished manuscript. 1996. https://algo.inria.fr/flajolet/Publications/landau.ps.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, pp. 9-10, 55, and 60-64, 1999.
Landau, E. "Über die Einteilung der positiven ganzen Zahlen in vier Klassen nach der Mindeszahl der zu ihrer additiven Zusammensetzung erforderlichen Quadrate." Arch. Math. Phys. 13, 305-312, 1908.
Landau, E. Handbuch der Lehre von der Verteilung der Primzahlen, Bd. II, 2nd ed. New York: Chelsea, pp. 641-669, 1953.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, 1983.
Moree, P. and Cazaran, J. "On a Claim of Ramanujan in His First Letter to Hardy." Expos. Math. 17, 289-312, 1999.
Selberg, A. Collected Papers, Vol. 2. Berlin: Springer-Verlag, pp. 183-185, 1991.
Shanks, D. "The Second-Order Term in the Asymptotic Expansion of 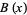 ." Math. Comput. 18, 75-86, 1964.
." Math. Comput. 18, 75-86, 1964.
Shanks, D. "Non-Hypotenuse Numbers." Fibonacci Quart. 13, 319-321, 1975.
Shanks, D. and Schmid, L. P. "Variations on a Theorem of Landau. I." Math. Comput. 20, 551-569, 1966.
Shiu, P. "Counting Sums of Two Squares: The Meissel-Lehmer Method." Math. Comput. 47, 351-360, 1986.
Sloane, N. J. A. Sequences A001481/M0968, A064533, A085990, and A164775 in "The On-Line Encyclopedia of Integer Sequences."
Stanley, G. K. "Two Assertions Made by Ramanujan." J. London Math. Soc. 3, 232-237, 1928.
Stanley, G. K. Corrigendum to "Two Assertions Made by Ramanujan." J. London Math. Soc. 4, 32, 1929.
Wolfram Research, Inc. "Computing the Landau-Ramanujan Constant." https://library.wolfram.com/infocenter/Demos/120/.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















