


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-10-2019
Date: 17-12-2020
Date: 7-1-2021
|
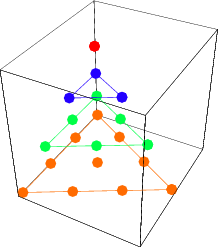
A figurate number 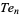 of the form
of the form
 |
 |
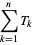 |
(1) |
 |
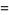 |
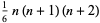 |
(2) |
 |
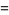 |
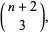 |
(3) |
where 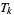 is the
is the 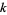 th triangular number and
th triangular number and 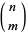 is a binomial coefficient. These numbers correspond to placing discrete points in the configuration of a tetrahedron (triangular base pyramid). Tetrahedral numbers are pyramidal numbers with
is a binomial coefficient. These numbers correspond to placing discrete points in the configuration of a tetrahedron (triangular base pyramid). Tetrahedral numbers are pyramidal numbers with 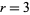 , and are the sum of consecutive triangular numbers. The first few are 1, 4, 10, 20, 35, 56, 84, 120, ... (OEIS A000292). The generating function for the tetrahedral numbers is
, and are the sum of consecutive triangular numbers. The first few are 1, 4, 10, 20, 35, 56, 84, 120, ... (OEIS A000292). The generating function for the tetrahedral numbers is
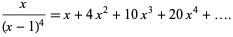 |
(4) |
Tetrahedral numbers are even, except for every fourth tetrahedral number, which is odd (Conway and Guy 1996).
The only numbers which are simultaneously square and tetrahedral are  ,
,  , and
, and 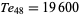 (giving
(giving 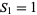 ,
, 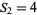 , and
, and  ), as proved by Meyl (1878; cited in Dickson 2005, p. 25).
), as proved by Meyl (1878; cited in Dickson 2005, p. 25).
Numbers which are simultaneously triangular and tetrahedral satisfy the binomial coefficient equation
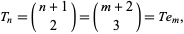 |
(5) |
the only solutions of which are
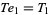 |
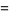 |
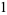 |
(6) |
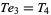 |
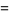 |
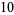 |
(7) |
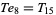 |
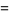 |
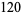 |
(8) |
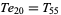 |
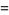 |
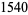 |
(9) |
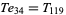 |
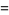 |
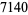 |
(10) |
(OEIS A027568; Avanesov 1966/1967; Mordell 1969, p. 258; Guy 1994, p. 147).
Beukers (1988) has studied the problem of finding numbers which are simultaneously tetrahedral and pyramidal via integer points on an elliptic curve, and finds that the only solution is the trivial 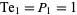 .
.
The minimum number of tetrahedral numbers needed to sum to 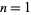 , 2, ... are given by 1, 2, 3, 1, 2, 3, 4, 2, 3, 1, ... (OEIS A104246). Pollock's conjecture states that every number is the sum of at most five tetrahedral numbers. The numbers that are not the sum of
, 2, ... are given by 1, 2, 3, 1, 2, 3, 4, 2, 3, 1, ... (OEIS A104246). Pollock's conjecture states that every number is the sum of at most five tetrahedral numbers. The numbers that are not the sum of 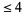 tetrahedral numbers are given by the sequence 17, 27, 33, 52, 73, ..., (OEIS A000797) containing 241 terms, with
tetrahedral numbers are given by the sequence 17, 27, 33, 52, 73, ..., (OEIS A000797) containing 241 terms, with 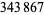 being almost certainly the last such number.
being almost certainly the last such number.
REFERENCES:
Avanesov, E. T. "Solution of a Problem on Figurate Numbers" [Russian]. Acta Arith. 12, 409-420, 1966/1967.
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 59, 1987.
Beukers, F. "On Oranges and Integral Points on Certain Plane Cubic Curves." Nieuw Arch. Wisk. 6, 203-210, 1988.
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 44-46, 1996.
Dickson, L. E. History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Dover, 2005.
Guy, R. K. "Figurate Numbers." §D3 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 147-150, 1994.
Meyl, A.-J.-J. "Solution de Question 1194." Nouv. Ann. Math. 17, 464-467, 1878.
Mordell, L. J. Diophantine Equations. New York: Academic Press, p. 258, 1969.
Skiena, S. S. The Algorithm Design Manual. New York: Springer-Verlag, pp. 43-45, 1997.
Sloane, N. J. A. Sequences A000292/M3382, A000797/M5033, A027568, and A104246 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
نقابة تمريض كربلاء تشيد بمستشفى الكفيل وتؤكّد أنّها بيئة تدريبية تمتلك معايير النجاح
|
|
|