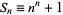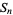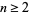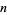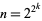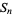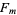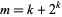A Sierpiński number of the first kind is a number of the form . The first few are 2, 5, 28, 257, 3126, 46657, 823544, 16777217, ... (OEIS A014566). Sierpiński proved that if  is prime with , then  must be of the form , making  a Fermat number  with . The first few  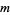of this form are 1, 3, 6, 11, 20, 37, 70, ... (OEIS A006127).

The numbers of digits in the number 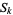 is given by

where  is the ceiling function, so the numbers of digits in the first few candidates are 1, 3, 20, 617, 315653, 41373247568, ... (OEIS A089943).

The only known prime Sierpiński numbers of the first kind are 2, 5, 257, with the first unknown case being 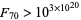. The status of Sierpiński numbers is summarized in the table below (Nielsen).

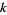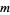		status of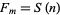
0	1	prime ()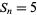
1	3	prime ()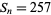
2	6	composite with factor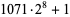
3	11	composite with factor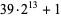
4	20	composite with no factor known
5	37	composite with factor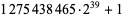
6	70	unknown
7	135	unknown
8	264	unknown
9	521	unknown
10	1034	unknown
11	2059	composite with factor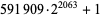
12	4108	unknown
13	8205	unknown
14	16398	unknown
15	32783	unknown
16	65552	unknown
17	131089	unknown

REFERENCES:

Keller, W. "Factors of Fermat Numbers and Large Primes of the Form 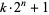." Math. Comput. 41, 661-673, 1983.

Keller, W. "Factors of Fermat Numbers and Large Primes of the Form 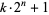, II." In prep.

Keller, W. "Prime Factors 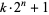 of Fermat Numbers  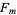and Complete Factoring Status." https://www.prothsearch.net/fermat.html.

Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, p. 155, 1979.

Nielsen, J. S. "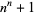." https://jeppesn.dk/nton.html.

Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, p. 74, 1989.

Sloane, N. J. A. Sequences A006127/M2547, A014566, A089943 in "The On-Line Encyclopedia of Integer Sequences."

اخر الاخبار

اخبار العتبة العباسية المقدسة

جولة تفقدية لمتابعة خطة تنظيم مداخل المعزّين المشاركين في عزاء ركضة طويريج

لتعزيز التعاون الأكاديمي والبحثي.. جامعة الكفيل توقع اتفاقيتي توأمة مع جامعتين عراقيتين

المجمَع العلميّ يواصل إقامة مجلسه العزائي بذكرى شهادة الإمام الحسين (عليه السلام) في النجف الأشرف

قسم حفظ النظام يواصل تنفيذ خطته لتنظيم سير المواكب والزائرين في شهر المحرم

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد