The 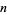th taxicab number  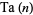is the smallest number representable in  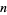ways as a sum of positive cubes. The numbers derive their name from the Hardy-Ramanujan number

			(1)
			(2)
			(3)

which is associated with a story told about Ramanujan by G. H. Hardy (Hofstadter 1989, Kanigel 1991, Snow 1993).

This property of 1729 was mentioned by the character Robert the sometimes insane mathematician, played by Anthony Hopkins, in the 2005 film Proof. It was also part of the designation of the spaceship Nimbus BP-1729 appearing in Season 2 of the animated television series Futurama episode DVD 2ACV02 (Greenwald; left figure), as well as the robot character Bender's serial number, as portrayed in a Christmas card in the episode Xmas Story (Volume 2 DVD, Georgoulias et al. 2004; right figure).

However, this property was also known as early as 1657 by F. de Bessy (Berndt and Bhargava 1993, Guy 1994). Leech (1957) found

			(4)
			(5)
			(6)
			(7)

Rosenstiel et al. (1991) recently found

			(8)
			(9)
			(10)
			(11)
			(12)

Wilson (1999) found

			(13)
			(14)
			(15)
			(16)
			(17)
			(18)

The first few taxicab numbers are therefore 2, 1729, 87539319, 6963472309248, 48988659276962496, ... (OEIS A011541).

The sixth taxicab number is

			(19)
			(20)
			(21)
			(22)
			(23)
			(24)
			(25)

(Calude et al. 2003, Hollerbach 2008).

Hardy and Wright (Theorem 412, 1979) show that the number of such sums can be made arbitrarily large but, updating Guy (1994) with Wilson's result, the least example is not known for six or more equal sums.

Sloane defines a slightly different type of taxicab numbers, namely numbers which are sums of two cubes in two or more ways, the first few of which are 1729, 4104, 13832, 20683, 32832, 39312, 40033, 46683, 64232, ... (OEIS A001235).

REFERENCES:

Berndt, B. C. and Bhargava, S. "Ramanujan--For Lowbrows." Am. Math. Monthly 100, 645-656, 1993.

Butler, B. "Ramanujan Numbers and the Taxicab Problem." https://www.durangobill.com/Ramanujan.html.

Calude,C. S.; Calude, E.; and Dinneen, M. J. "What Is the Value of Taxicab(6)?" J. Uni. Comp. Sci. 9, 1196-1203, 2003. https://www.cs.auckland.ac.nz/~cristian/taxicab.pdf.

Georgoulias, T.; Greenwald, S. J.; and Wichterich, M. "Futurama : Mathematics in the Year 3000." Math Horizons, 12-15, Apr. 2004.

Greenwald, S. "Dr. Sarah's Futurama 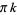--Mathematics in the Year 3000." https://www.mathsci.appstate.edu/~sjg/futurama/.

Guy, R. K. "Sums of Like Powers. Euler's Conjecture." §D1 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 139-144, 1994.

Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, pp. 12 and 68, 1999.

Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.

Hofstadter, D. R. Gödel, Escher, Bach: An Eternal Golden Braid. New York: Vintage Books, p. 564, 1989.

Hollerbach, U. "The Sixth Taxicab Number Is 24153319581254312065344." Mar. 8, 2008. https://listserv.nodak.edu/cgi-bin/wa.exe?A2=ind0803&L=nmbrthry&T=0&F=&S=&P=1059.

Kanigel, R. The Man Who Knew Infinity: A Life of the Genius Ramanujan. New York: Washington Square Press, p. 312, 1991.

Leech, J. "Some Solutions of Diophantine Equations." Proc. Cambridge Phil. Soc. 53, 778-780, 1957.

Meyrignac, J. "The Taxicab Problem." https://euler.free.fr/taxicab.htm.

Plouffe, S. "Taxicab Numbers." https://pi.lacim.uqam.ca/eng/problem_en.html.

Rosenstiel, E.; Dardis, J. A.; and Rosenstiel, C. R. "The Four Least Solutions in Distinct Positive Integers of the Diophantine Equation 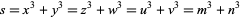." Bull. Inst. Math. Appl. 27, 155-157, 1991.

Silverman, J. H. "Taxicabs and Sums of Two Cubes." Amer. Math. Monthly 100, 331-340, 1993.

Sloane, N. J. A. Sequences A001235 and A011541 in "The On-Line Encyclopedia of Integer Sequences."

Snow, C. P. Foreword to A Mathematician's Apology, reprinted with a foreword by C. P. Snow (by G. H. Hardy). New York: Cambridge University Press, p. 37, 1993.

Wilson, D. W. "The Fifth Taxicab Number is 48988659276962496." J. Integer Sequences 2, #99.1.9, 1999.

Wooley, T. D. "Sums of Two Cubes." Internat. Math. Res. Not. No. 4, 181-184, 1995.

اخر الاخبار

اخبار العتبة العباسية المقدسة

جولة تفقدية لمتابعة خطة تنظيم مداخل المعزّين المشاركين في عزاء ركضة طويريج

لتعزيز التعاون الأكاديمي والبحثي.. جامعة الكفيل توقع اتفاقيتي توأمة مع جامعتين عراقيتين

المجمَع العلميّ يواصل إقامة مجلسه العزائي بذكرى شهادة الإمام الحسين (عليه السلام) في النجف الأشرف

قسم حفظ النظام يواصل تنفيذ خطته لتنظيم سير المواكب والزائرين في شهر المحرم

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد