


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-1-2021
Date: 6-4-2020
Date: 9-9-2020
|
Consider the Fibonacci-like recurrence
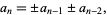 |
(1) |
where 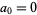 ,
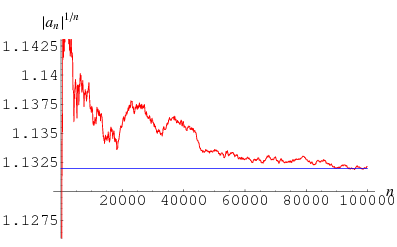
, 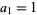 , and each sign is chosen independently and at random with probability 1/2. Surprisingly, Viswanath (2000) showed that
, and each sign is chosen independently and at random with probability 1/2. Surprisingly, Viswanath (2000) showed that
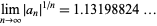 |
(2) |
(OEIS A078416) with probability one. This constant is sometimes known as Viswanath's constant.
Considering the more general recurrence
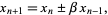 |
(3) |
the limit
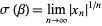 |
(4) |
exists for almost all values of 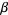 . The critical value
. The critical value 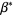 such that
such that 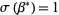 is given by
is given by
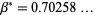 |
(5) |
(OEIS A118288) and is sometimes known as the Embree-Trefethen constant.
Since Fibonacci numbers can be computed as products of Fibonacci Q-matrices, this same constant arises in the iterated multiplication of certain pairs of 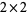 random matrices (Bougerol and Lacrois 1985, pp. 11 and 157).
random matrices (Bougerol and Lacrois 1985, pp. 11 and 157).
REFERENCES:
Batista Oliveira, J. and De Figueiredo, L. H. "Interval Computation of Viswanath's Constant." Reliab. Comput. 8, 131-138, 2002.
Bougerol, P. and Lacrois, J. Random Products of Matrices With Applications to Infinite-Dimensional Schrödinger Operators. Basel, Switzerland: Birkhäuser, 1985.
Devlin, K. "Devlin's Angle: New Mathematical Constant Discovered: Descendent of Two Thirteenth Century Rabbits." March 1999. https://www.maa.org/devlin/devlin_3_99.html.
Embree, M. and Trefethen, L. N. "Growth and Decay of Random Fibonacci Sequences." Roy. Soc. London Proc. Ser. A, Math. Phys. Eng. Sci. 455, 2471-2485, 1999.
Livio, M. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number. New York: Broadway Books, pp. 227-228, 2002.
Michon, G. P. "Final Answers: Numerical Constants." https://home.att.net/~numericana/answer/constants.htm#viswanath.
Peterson, I. "Fibonacci at Random: Uncovering a New Mathematical Constant." Sci. News 155, 376, June 12, 1999. https://sciencenews.org/sn_arc99/6_12_99/bob1.htm.
Sloane, N. J. A. Sequences A078416 and A118288 in "The On-Line Encyclopedia of Integer Sequences."
Viswanath, D. "Random Fibonacci Sequences and the Number 1.13198824...." Math. Comput. 69, 1131-1155, 2000.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
ضمن أسبوع الإرشاد النفسي.. جامعة العميد تُقيم أنشطةً ثقافية وتطويرية لطلبتها
|
|
|