المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Boole Polynomial |
 1925
 05:04 مساءً
date: 17-9-2019 |
Author : Boas, R. P. and Buck, R. C. 
Book or Source : Polynomial Expansions of Analytic Functions, 2nd print., corr. New York: Academic Press 
Page and Part : ...|
Read More
Date: 10-10-2019
1815
Date: 19-9-2018
1691
Date: 30-3-2019
1455
|
Polynomials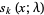 
which form a Sheffer sequence with
 |
 |
 |
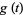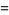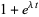(1) |
 |
 |
 |
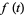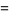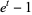(2) |
and have generating function
 |
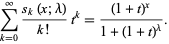(3) |
The first few are
 |
 |
 |
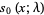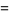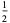(4) |
 |
 |
 |
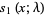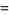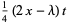(5) |
 |
 |
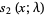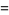![1/4[2x(x-lambda-1)+lambda].](http://mathworld.wolfram.com/images/equations/BoolePolynomial/Inline16.gif) |
(6) |
Jordan (1965) considers the related polynomials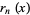 
which form a Sheffer sequence with
 |
 |
 |
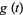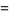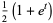(7) |
 |
 |
 |
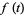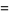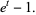(8) |
These polynomials have generating function
 |
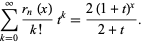(9) |
The first few are
 |
 |
 |
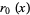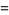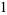(10) |
 |
 |
 |
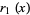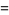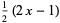(11) |
 |
 |
 |
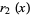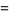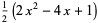(12) |
 |
 |
 |
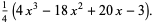(13) |
The Peters polynomials are a generalization of the Boole polynomials.
REFERENCES:
Boas, R. P. and Buck, R. C. Polynomial Expansions of Analytic Functions, 2nd print., corr. New York: Academic Press, p. 37, 1964.
Jordan, C. Calculus of Finite Differences, 3rd ed. New York: Chelsea, 1965.
Roman, S. The Umbral Calculus. New York: Academic Press, 1984.
|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
بالصور: ممثل المرجعية العليا والامين العام للعتبة الحسينية يستقبلون المهنئين القاصدين مرقد الامام الحسين (ع) في عيد الفطر المبارك
|
|
|
