


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-1-2020
Date: 28-8-2020
Date: 22-4-2020
|
The Jacobsthal numbers are the numbers obtained by the 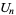 s in the Lucas sequence with
s in the Lucas sequence with 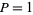 and
and 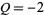 , corresponding to
, corresponding to 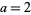 and
and 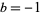 . They and the Jacobsthal-Lucas numbers (the
. They and the Jacobsthal-Lucas numbers (the 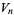 s) satisfy the recurrence relation
s) satisfy the recurrence relation
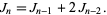 |
(1) |
The Jacobsthal numbers satisfy 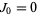 and
and 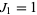 and are 0, 1, 1, 3, 5, 11, 21, 43, 85, 171, 341, ... (OEIS A001045). The Jacobsthal-Lucas numbers satisfy
and are 0, 1, 1, 3, 5, 11, 21, 43, 85, 171, 341, ... (OEIS A001045). The Jacobsthal-Lucas numbers satisfy 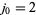 and
and 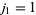 and are 2, 1, 5, 7, 17, 31, 65, 127, 257, 511, 1025, ... (OEIS A014551). The properties of these numbers are summarized in Horadam (1996).
and are 2, 1, 5, 7, 17, 31, 65, 127, 257, 511, 1025, ... (OEIS A014551). The properties of these numbers are summarized in Horadam (1996).
Microcontrollers (and other computers) use conditional instructions to change the flow of execution of a program. In addition to branch instructions, some microcontrollers use skip instructions which conditionally bypass the next instruction. This winds up being useful for one case out of the four possibilities on 2 bits, 3 cases on 3 bits, 5 cases on 4 bits, 11 on 5 bits, 21 on 6 bits, 43 on 7 bits, 85 on 8 bits, ..., which are exactly the Jacobsthal numbers (Hirst 2006).
The Jacobsthal and Jacobsthal-Lucas numbers are given by the closed form expressions
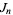 |
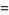 |
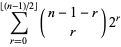 |
(2) |
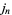 |
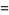 |
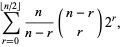 |
(3) |
where 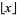 is the floor function and
is the floor function and 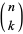 is a binomial coefficient. The Binet forms are
is a binomial coefficient. The Binet forms are
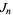 |
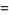 |
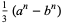 |
(4) |
 |
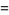 |
![1/3[2^n-(-1)^n]](https://mathworld.wolfram.com/images/equations/JacobsthalNumber/Inline24.gif) |
(5) |
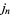 |
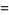 |
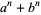 |
(6) |
 |
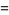 |
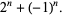 |
(7) |
Amazingly, when interpreted in binary, the Jacobsthal numbers 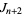 give the
give the  th iteration of applying the rule 28 cellular automaton to initial conditions consisting of a single black cell (E. W. Weisstein, Apr. 12, 2006).
th iteration of applying the rule 28 cellular automaton to initial conditions consisting of a single black cell (E. W. Weisstein, Apr. 12, 2006).
The generating functions are
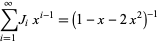 |
(8) |
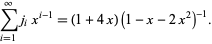 |
(9) |
The Simson formulas are
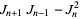 |
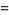 |
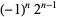 |
(10) |
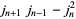 |
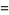 |
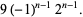 |
(11) |
Summation formulas include
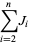 |
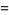 |
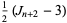 |
(12) |
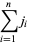 |
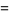 |
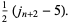 |
(13) |
Interrelationships are
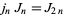 |
(14) |
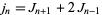 |
(15) |
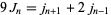 |
(16) |
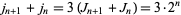 |
(17) |
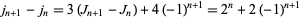 |
(18) |
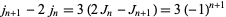 |
(19) |
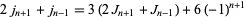 |
(20) |
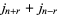 |
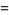 |
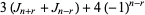 |
(21) |
 |
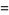 |
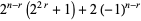 |
(22) |
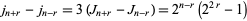 |
(23) |
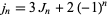 |
(24) |
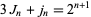 |
(25) |
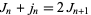 |
(26) |
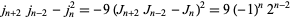 |
(27) |
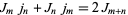 |
(28) |
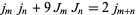 |
(29) |
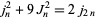 |
(30) |
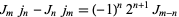 |
(31) |
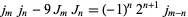 |
(32) |
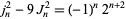 |
(33) |
(Horadam 1996).
REFERENCES:
Bergum, G. E.; Bennett, L.; Horadam, A. F.; and Moore, S. D. "Jacobsthal Polynomials and a Conjecture Concerning Fibonacci-Like Matrices." Fib. Quart. 23, 240-248, 1985.
Hirst, C. "Hopscotch--Multiple Bit Testing." May 15, 2006. https://www.avrfreaks.net/index.php?module=FreaksAcademy&func=viewItem&item_id=229&item_type=project.
Horadam, A. F. "Jacobsthal and Pell Curves." Fib. Quart. 26, 79-83, 1988.
Horadam, A. F. "Jacobsthal Representation Numbers." Fib. Quart. 34, 40-54, 1996.
Sloane, N. J. A. Sequences A001045/M2482 and A014551 in "The On-Line Encyclopedia of Integer Sequences."
Hoggatt and Bicknell, in ÒConvolution Triangles,Ó FQ 10 (1972), 599-608),



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|