

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Smarandache Function
المؤلف:
Akbik, S.
المصدر:
"On a Density Problem of Erdős." Int. J. Math. Sci. 22
الجزء والصفحة:
...
29-11-2020
1013
Smarandache Function
The Smarandache function 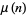 is the function first considered by Lucas (1883), Neuberg (1887), and Kempner (1918) and subsequently rediscovered by Smarandache (1980) that gives the smallest value for a given
is the function first considered by Lucas (1883), Neuberg (1887), and Kempner (1918) and subsequently rediscovered by Smarandache (1980) that gives the smallest value for a given 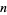 at which
at which 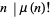 (i.e.,
(i.e., 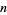 divides
divides 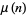 factorial). For example, the number 8 does not divide
factorial). For example, the number 8 does not divide 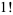 ,
, 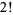 ,
, 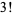 , but does divide
, but does divide 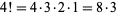 , so
, so 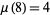 .
.
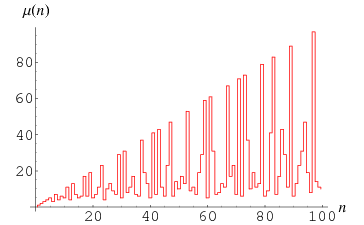
For  , 2, ...,
, 2, ..., 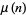 is given by 1, 2, 3, 4, 5, 3, 7, 4, 6, 5, 11, ... (OEIS A002034), where it should be noted that Sloane defines
is given by 1, 2, 3, 4, 5, 3, 7, 4, 6, 5, 11, ... (OEIS A002034), where it should be noted that Sloane defines 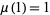 , while Ashbacher (1995) and Russo (2000, p. 4) take
, while Ashbacher (1995) and Russo (2000, p. 4) take 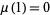 . The incrementally largest values of
. The incrementally largest values of 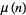 are 1, 2, 3, 4, 5, 7, 11, 13, 17, 19, 23, 29, ... (OEIS A046022), which occur at the values where
are 1, 2, 3, 4, 5, 7, 11, 13, 17, 19, 23, 29, ... (OEIS A046022), which occur at the values where 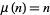 . The incrementally smallest values of
. The incrementally smallest values of 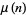 relative to
relative to 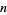 are
are 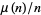 = 1, 1/2, 1/3, 1/4, 1/6, 1/8, 1/12, 3/40, 1/15, 1/16, 1/24, 1/30, ... (OEIS A094404 and A094372), which occur at
= 1, 1/2, 1/3, 1/4, 1/6, 1/8, 1/12, 3/40, 1/15, 1/16, 1/24, 1/30, ... (OEIS A094404 and A094372), which occur at 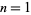 , 6, 12, 20, 24, 40, 60, 80, 90, 112, 120, 180, ... (OEIS A094371).
, 6, 12, 20, 24, 40, 60, 80, 90, 112, 120, 180, ... (OEIS A094371).
Formulas exist for immediately computing 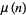 for special forms of
for special forms of 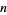 . The simplest cases are
. The simplest cases are
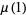 |
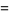 |
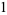 |
(1) |
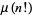 |
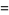 |
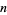 |
(2) |
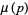 |
 |
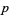 |
(3) |
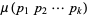 |
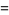 |
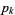 |
(4) |
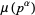 |
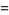 |
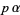 |
(5) |
where 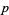 is a prime,
is a prime, 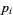 are distinct primes,
are distinct primes, 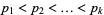 , and
, and 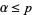 (Kempner 1918). In addition,
(Kempner 1918). In addition,
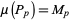 |
(6) |
if 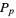 is the
is the 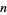 th even perfect number and
th even perfect number and 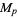 is the corresponding Mersenne prime (Ashbacher 1997; Ruiz 1999a). Finally, if
is the corresponding Mersenne prime (Ashbacher 1997; Ruiz 1999a). Finally, if 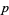 is a prime number and
is a prime number and 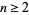 an integer, then
an integer, then
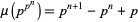 |
(7) |
(Ruiz 1999b).
The case 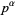 for
for 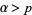 is more complicated, but can be computed by an algorithm due to Kempner (1918). To begin, define
is more complicated, but can be computed by an algorithm due to Kempner (1918). To begin, define 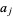 recursively by
recursively by
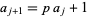 |
(8) |
with 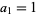 . This can be solved in closed form as
. This can be solved in closed form as
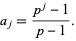 |
(9) |
Now find the value of  such that
such that 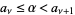 , which is given by
, which is given by
![nu=|_log_p[1+alpha(p-1)]_|,](https://mathworld.wolfram.com/images/equations/SmarandacheFunction/NumberedEquation5.gif) |
(10) |
where 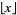 is the floor function. Now compute the sequences
is the floor function. Now compute the sequences 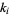 and
and 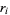 according to the Euclidean algorithm-like procedure
according to the Euclidean algorithm-like procedure
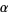 |
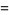 |
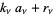 |
(11) |
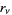 |
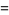 |
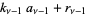 |
(12) |
 |
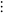 |
 |
(13) |
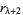 |
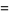 |
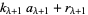 |
(14) |
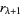 |
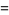 |
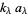 |
(15) |
i.e., until the remainder 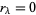 . At each step,
. At each step, 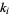 is the integer part of
is the integer part of 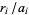 and
and 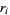 is the remainder. For example, in the first step,
is the remainder. For example, in the first step, 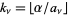 and
and 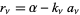 . Then
. Then
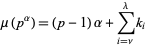 |
(16) |
(Kempner 1918).
The value of 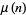 for general
for general 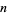 is then given by
is then given by
![mu(p_1^(alpha_1)p_2^(alpha_2)...p_r^(alpha_r))=max[mu(p_1^(alpha_1)),mu(p_2^(alpha_2)),...,mu(p_r^(alpha_r))]](https://mathworld.wolfram.com/images/equations/SmarandacheFunction/NumberedEquation7.gif) |
(17) |
(Kempner 1918).
For all 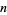
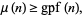 |
(18) |
where 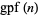 is the greatest prime factor of
is the greatest prime factor of 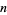 .
.
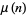 can be computed by finding
can be computed by finding 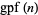 and testing if
and testing if 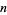 divides
divides 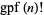 . If it does, then
. If it does, then 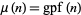 . If it doesn't, then
. If it doesn't, then 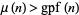 and Kempner's algorithm must be used. The set of
and Kempner's algorithm must be used. The set of 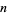 for which
for which 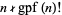 (i.e.,
(i.e., 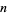 does not divide
does not divide 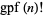 ) has density zero as proposed by Erdős (1991) and proved by Kastanas (1994), but for small
) has density zero as proposed by Erdős (1991) and proved by Kastanas (1994), but for small 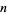 , there are quite a large number of values for which
, there are quite a large number of values for which 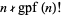 . The first few of these are 4, 8, 9, 12, 16, 18, 24, 25, 27, 32, 36, 45, 48, 49, 50, ... (OEIS A057109). Letting
. The first few of these are 4, 8, 9, 12, 16, 18, 24, 25, 27, 32, 36, 45, 48, 49, 50, ... (OEIS A057109). Letting 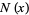 denote the number of positive integers
denote the number of positive integers 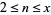 such that
such that 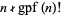 , Akbik (1999) subsequently showed that
, Akbik (1999) subsequently showed that
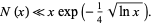 |
(19) |
This was subsequently improved by Ford (1999) and De Koninck and Doyon (2003), the former of which is unfortunately incorrect. Ford (1999) proposed the asymptotic formula
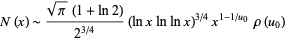 |
(20) |
where 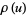 is the Dickman function,
is the Dickman function, 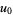 is defined implicitly through
is defined implicitly through
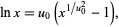 |
(21) |
and the constant needs correction (Ivić 2003). Ivić (2003) subsequently showed that
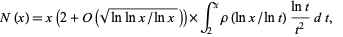 |
(22) |
and, in terms of elementary functions,
![N(x)=xexp[-sqrt(2lnxlnlnx)(1+O(lnlnlnx/lnlnx))].](https://mathworld.wolfram.com/images/equations/SmarandacheFunction/NumberedEquation13.gif) |
(23) |
Tutescu (1996) conjectured that 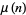 never takes the same value for two consecutive arguments, i.e.,
never takes the same value for two consecutive arguments, i.e., 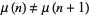 for any
for any 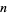 . This holds up to at least
. This holds up to at least 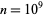 (Weisstein, Mar. 3, 2004).
(Weisstein, Mar. 3, 2004).
Multiple values of 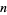 can have the same value of
can have the same value of 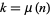 , as summarized in the following table for small
, as summarized in the following table for small 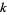 .
.
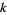 |
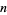 such that such that 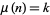 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3, 6 |
| 4 | 4, 8, 12, 24 |
| 5 | 5, 10, 15, 20, 30, 40, 60, 120 |
| 6 | 9, 16, 18, 36, 45, 48, 72, 80, 90, 144, 180, 240, 360, 720 |
Let 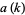 denote the smallest inverse of
denote the smallest inverse of 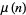 , i.e., the smallest
, i.e., the smallest 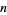 for which
for which 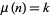 . Then
. Then 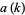 is given by
is given by
![a(k)=[gpf(k)]^(e+1),](https://mathworld.wolfram.com/images/equations/SmarandacheFunction/NumberedEquation14.gif) |
(24) |
where
![e=sum_(i=1)^(|_log_(gpf(k))(n-1)_|)|_(n-1)/([gpf(k)]^i)_|](https://mathworld.wolfram.com/images/equations/SmarandacheFunction/NumberedEquation15.gif) |
(25) |
(J. Sondow, pers. comm., Jan. 17, 2005), where 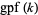 is the greatest prime factor of
is the greatest prime factor of 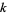 and
and 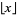 is the floor function. For
is the floor function. For 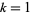 , 2, ...,
, 2, ..., 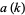 is given by 1, 2, 3, 4, 5, 9, 7, 32, 27, 25, 11, 243, ... (OEIS A046021). Some values of
is given by 1, 2, 3, 4, 5, 9, 7, 32, 27, 25, 11, 243, ... (OEIS A046021). Some values of 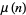 first occur only for very large
first occur only for very large 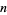 . The sequence of incrementally largest values of
. The sequence of incrementally largest values of 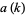 is 1, 2, 3, 4, 5, 9, 32, 243, 4096, 59049, 177147, 134217728, ... (OEIS A092233), corresponding to
is 1, 2, 3, 4, 5, 9, 32, 243, 4096, 59049, 177147, 134217728, ... (OEIS A092233), corresponding to 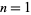 , 2, 3, 4, 5, 6, 8, 12, 16, 24, 27, 32, ... (OEIS A092232).
, 2, 3, 4, 5, 6, 8, 12, 16, 24, 27, 32, ... (OEIS A092232).
To find the number of 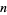 for which
for which 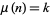 , note that by definition,
, note that by definition, 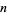 is a divisor of
is a divisor of 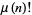 but not of
but not of 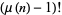 . Therefore, to find all
. Therefore, to find all 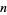 for which
for which 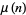 has a given value, say all
has a given value, say all 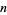 with
with 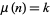 , take the set of all divisors of
, take the set of all divisors of 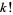 and omit the divisors of
and omit the divisors of 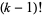 . In particular, the number
. In particular, the number 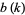 of
of 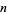 for which
for which 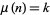 for
for 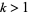 is exactly
is exactly
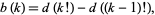 |
(26) |
where 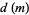 denotes the number of divisors of
denotes the number of divisors of 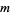 , i.e., the divisor function
, i.e., the divisor function 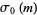 . Therefore, the numbers of integers
. Therefore, the numbers of integers 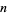 with
with 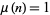 , 2, ... are given by 1, 1, 2, 4, 8, 14, 30, 36, 64, 110, ... (OEIS A038024).
, 2, ... are given by 1, 1, 2, 4, 8, 14, 30, 36, 64, 110, ... (OEIS A038024).
In particular, equation (26) shows that the inverse Smarandache function 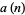 always exists since for every
always exists since for every 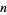 there is an
there is an 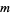 with
with 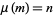 (hence a smallest one a(n)), since
(hence a smallest one a(n)), since 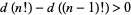 for
for 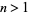 .
.
Sondow (2006) showed that 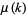 unexpectedly arises in an irrationality bound for e, and conjectures that the inequality
unexpectedly arises in an irrationality bound for e, and conjectures that the inequality 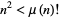 holds for almost all
holds for almost all 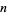 , where "for almost all" means except for a set of density zero. The exceptions are 2, 3, 6, 8, 12, 15, 20, 24, 30, 36, 40, 45, 48, 60, 72, 80, ... (OEIS A122378).
, where "for almost all" means except for a set of density zero. The exceptions are 2, 3, 6, 8, 12, 15, 20, 24, 30, 36, 40, 45, 48, 60, 72, 80, ... (OEIS A122378).
Since 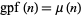 for almost all
for almost all 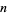 (Erdős 1991, Kastanas 1994), where
(Erdős 1991, Kastanas 1994), where 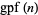 is the greatest prime factor, an equivalent conjecture is that the inequality
is the greatest prime factor, an equivalent conjecture is that the inequality 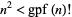 holds for almost all
holds for almost all 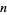 . The exceptions are 2, 3, 4, 6, 8, 9, 12, 15, 16, 18, 20, 24, 25, 27, 30, 32, 36, ... (OEIS A122380).
. The exceptions are 2, 3, 4, 6, 8, 9, 12, 15, 16, 18, 20, 24, 25, 27, 30, 32, 36, ... (OEIS A122380).
D. Wilson points out that if
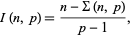 |
(27) |
is the power of the prime 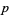 in
in 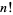 , where
, where 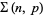 is the sum of the base-
is the sum of the base-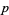 digits of
digits of 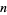 , then it follows that
, then it follows that
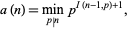 |
(28) |
where the minimum is taken over the primes 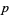 dividing
dividing 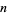 . This minimum appears to always be achieved when
. This minimum appears to always be achieved when 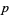 is the greatest prime factor of
is the greatest prime factor of 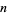 .
.
REFERENCES:
Akbik, S. "On a Density Problem of Erdős." Int. J. Math. Sci. 22, 655-658, 1999.
Ashbacher, C. An Introduction to the Smarandache Function. Cedar Rapids, IA: Decisionmark, 1995.
Ashbacher, C. "Problem 4616." School Sci. Math. 97, 221, 1997.
Begay, A. "Smarandache Ceil Functions." Bulletin Pure Appl. Sci. India 16E, 227-229, 1997.
De Koninck, J.-M. and Doyon, N. "On a Thin Set of Integers Involving the Largest Prime Factor Function." Int. J. Math. Math. Sci., No. 19, 1185-1192, 2003.
Dumitrescu, C. and Seleacu, V. The Smarandache Function. Vail, AZ: Erhus University Press, 1996.
Erdős, P. "Problem 6674." Amer. Math. Monthly 98, 965, 1991.
Finch, S. "The Average Value of the Smarandache Function." Smarandache Notions J. 10, 95-96, 1999. https://www.gallup.unm.edu/~smarandache/SNBook10.pdf.
Finch, S. "Moments of the Smarandache Function." Smarandache Notions J. 11, 140-141, 2000. https://www.gallup.unm.edu/~smarandache/SNBook11.pdf.
Finch, S. R. "Golomb-Dickman Constant." §5.4 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 284-292, 2003.
Ford, K. "The Normal Behavior of the Smarandache Function." Smarandache Notions J. 10, 81-86, 1999. https://www.gallup.unm.edu/~smarandache/SNBook10.pdf.
"Functions in Number Theory." https://www.gallup.unm.edu/~smarandache/FUNCT1.TXT.
Hungerbühler, N. and Specker, E. "A Generalization of the Smarandache Function to Several Variables." Integers: Electronic J. Combin. Number Th. 6, #A23, 2006 https://www.integers-ejcnt.org/vol6.html.
Ibstedt, H. Surfing on the Ocean of Numbers--A Few Smarandache Notions and Similar Topics. Lupton, AZ: Erhus University Press, pp. 27-30, 1997.
Ivić, A. "On a Problem of Erdős Involving the Largest Prime Factor of 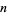 ." 5 Nov 2003. https://arxiv.org/abs/math.NT/0311056.
." 5 Nov 2003. https://arxiv.org/abs/math.NT/0311056.
Kastanas, I. "Solution to Problem 6674: The Smallest Factorial That Is a Multiple of 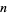 ." Amer. Math. Monthly 101, 179, 1994.
." Amer. Math. Monthly 101, 179, 1994.
Kempner, A. J. "Miscellanea." Amer. Math. Monthly 25, 201-210, 1918.
Lucas, E. "Question Nr. 288." Mathesis 3, 232, 1883.
Neuberg, J. "Solutions de questions proposées, Question Nr. 288." Mathesis 7, 68-69, 1887.
Ruiz, S. M. "Smarandache Function Applied to Perfect Numbers." Smarandache Notions J. 10, 114-155, 1999a.
Ruiz, S. M. "A Result Obtained Using Smarandache Function." Smarandache Notions J. 10, 123-124, 1999b.
Russo, F. A Set of New Smarandache Functions, Sequences, and Conjectures in Numer Theory. Lupton, AZ: American Research Press, 2000.
Sandor, J. "On Certain Inequalities Involving the Smarandache Function." Abstracts of Papers Presented to the Amer. Math. Soc. 17, 583, 1996.
Sloane, N. J. A. Sequences A002034/M0453, A038024, A046021, A046022, A057109, A092232, A092233, A094371, A094372, A094404, A122378, and A122380 in "The On-Line Encyclopedia of Integer Sequences."
Smarandache, F. "A Function in Number Theory." Analele Univ. Timisoara, Ser. St. Math. 43, 79-88, 1980.
Smarandache, F. Collected Papers, Vol. 1. Bucharest, Romania: Tempus, 1996.
Smarandache, F. Collected Papers, Vol. 2. Kishinev, Moldova: Kishinev University Press, 1997.
Sondow, J. "A Geometric Proof that 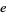 Is Irrational and a New Measure of Its Irrationality." Amer. Math. Monthly 113, 637-641, 2006.
Is Irrational and a New Measure of Its Irrationality." Amer. Math. Monthly 113, 637-641, 2006.
Tutescu, L. "On a Conjecture Concerning the Smarandache Function." Abstracts of Papers Presented to the Amer. Math. Soc. 17, 583, 1996.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















