


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-11-2019
Date: 26-9-2020
Date: 1-11-2019
|
The numbers 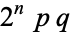 and
and 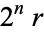 are an amicable pair if the three integers
are an amicable pair if the three integers
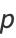 |
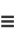 |
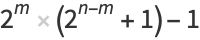 |
(1) |
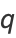 |
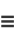 |
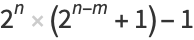 |
(2) |
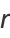 |
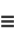 |
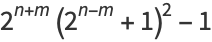 |
(3) |
are all prime numbers for some positive integer 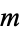 satisfying
satisfying 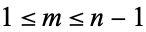 (Dickson 2005, p. 42). However, there are many amicable pairs which do not satisfy Euler's rule, so it is a sufficient but not necessary condition for amicability. Euler's rule is a generalization of Thâbit ibn Kurrah rule.
(Dickson 2005, p. 42). However, there are many amicable pairs which do not satisfy Euler's rule, so it is a sufficient but not necessary condition for amicability. Euler's rule is a generalization of Thâbit ibn Kurrah rule.
The first few 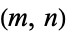 for which Euler's rule is satisfied are
for which Euler's rule is satisfied are 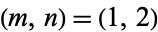 ,
, 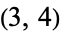 ,
, 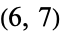 ,
, 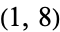 ,
, 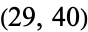 , ... (OEIS A094445 and A094446), with no others for
, ... (OEIS A094445 and A094446), with no others for 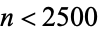 , corresponding to the triples
, corresponding to the triples 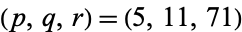 , (23, 47, 1151), (191, 383, 73727), ..., giving the amicable pairs (220, 284), (17296, 18416), (9363584, 9437056), ....
, (23, 47, 1151), (191, 383, 73727), ..., giving the amicable pairs (220, 284), (17296, 18416), (9363584, 9437056), ....
REFERENCES:
Borho, W. "On Thabit ibn Kurrah's Formula for Amicable Numbers." Math. Comput. 26, 571-578, 1972.
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, 2005.
Euler, L. "De Numeris Amicabilibus." In Opera Omnia, Series Prima, Vol. 2. Leipzig, Germany: Teubner, pp. 63-162, 1915.
Sloane, N. J. A. Sequences A094445 and A094446 in "The On-Line Encyclopedia of Integer Sequences."
te Riele, H. J. J. "Four Large Amicable Pairs." Math. Comput. 28, 309-312, 1974.a



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|