


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-7-2020
Date: 2-4-2020
Date: 24-11-2019
|
An integer 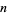 such that
such that 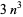 contains three consecutive 3s in its decimal representation is called a super-3 number. The first few super-3 numbers are 261, 462, 471, 481, 558, 753, 1036, ... (OEIS A014569). A. Anderson has shown that all numbers ending in 471, 4710, or 47100 are super-3 (Pickover 1995).
contains three consecutive 3s in its decimal representation is called a super-3 number. The first few super-3 numbers are 261, 462, 471, 481, 558, 753, 1036, ... (OEIS A014569). A. Anderson has shown that all numbers ending in 471, 4710, or 47100 are super-3 (Pickover 1995).
In general, a super-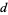 number is a number
number is a number 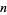 such that
such that 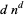 contains
contains 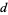
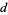 s in its decimal representation. The following table gives the first few super-
s in its decimal representation. The following table gives the first few super-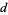 numbers for small
numbers for small 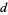 .
.
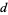 |
OEIS | super-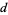 numbers numbers |
| 2 | A032743 | 19, 31, 69, 81, 105, 106, 107, 119, ... |
| 3 | A014569 | 261, 462, 471, 481, 558, 753, 1036, ... |
| 4 | A032744 | 1168, 4972, 7423, 7752, 8431, 10267, ... |
| 5 | A032745 | 4602, 5517, 7539, 12955, 14555, 20137, ... |
| 6 | A032746 | 27257, 272570, 302693, 323576, ... |
| 7 | A032747 | 140997, 490996, 1184321, 1259609, ... |
| 8 | A032748 | 185423, 641519, 1551728, 1854230, ... |
| 9 | A032749 | 17546133, 32613656, 93568867, ... |
The following table gives the first few palindromic super-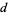 numbers for small
numbers for small 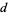 .
.
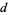 |
OEIS | palindromic super-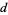 numbers numbers |
| 2 | A032750 | 131, 181, 333, 454, 919, 969, 1331, ... |
| 3 | A032751 | 4554, 6776, 17471, 22322, 22722, 28182, 43434, ... |
| 4 | A032752 | 83338, 1142411, 1571751, 1587851, 2013102, ... |
| 5 | A032753 | 3975793, 9799979, 39199193, 41299214, 65455456, ... |
| 6 | A032754 | 2023202, 374929473, 458353854, 499202994, 749858947, ... |
REFERENCES:
Pickover, C. A. Keys to Infinity. New York: Wiley, p. 7, 1995.
Sloane, N. J. A. Sequences A014569, A032743, A032744, A032745, A032746, A032747, A032748, A032749, A032750, A032751, A032752, A032753, A032754, A032755, and A032756 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|