


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-11-2019
Date: 11-8-2020
Date: 4-11-2020
|
An 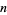 -digit number that is the sum of the
-digit number that is the sum of the  th powers of its digits is called an
th powers of its digits is called an 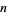 -narcissistic number. It is also sometimes known as an Armstrong number, perfect digital invariant (Madachy 1979), or plus perfect number. Hardy (1993) wrote, "There are just four numbers, after unity, which are the sums of the cubes of their digits:
-narcissistic number. It is also sometimes known as an Armstrong number, perfect digital invariant (Madachy 1979), or plus perfect number. Hardy (1993) wrote, "There are just four numbers, after unity, which are the sums of the cubes of their digits: 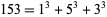 ,
, 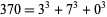 ,
, 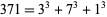 , and
, and 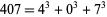 . These are odd facts, very suitable for puzzle columns and likely to amuse amateurs, but there is nothing in them which appeals to the mathematician." Narcissistic numbers therefore generalize these "unappealing" numbers to other powers (Madachy 1979, p. 164).
. These are odd facts, very suitable for puzzle columns and likely to amuse amateurs, but there is nothing in them which appeals to the mathematician." Narcissistic numbers therefore generalize these "unappealing" numbers to other powers (Madachy 1979, p. 164).
The smallest example of a narcissistic number other than the trivial 1-digit numbers is
 |
(1) |
The first few are given by 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407, 1634, 8208, 9474, 54748, ... (OEIS A005188).
It can easily be shown that base-10 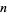 -narcissistic numbers can exist only for
-narcissistic numbers can exist only for 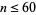 , since
, since
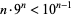 |
(2) |
for 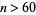 . In fact, as summarized in the table below, a total of 88 narcissistic numbers exist in base 10, as proved by D. Winter in 1985 and verified by D. Hoey. T. A. Mendes Oliveira e Silva gave the full sequence in a posting (Article 42889) to sci.math on May 9, 1994. These numbers exist for only 1, 3, 4, 5, 6, 7, 8, 9, 10, 11, 14, 16, 17, 19, 20, 21, 23, 24, 25, 27, 29, 31, 32, 33, 34, 35, 37, 38, and 39 (OEIS A114904) digits, and the series of smallest narcissistic numbers of
. In fact, as summarized in the table below, a total of 88 narcissistic numbers exist in base 10, as proved by D. Winter in 1985 and verified by D. Hoey. T. A. Mendes Oliveira e Silva gave the full sequence in a posting (Article 42889) to sci.math on May 9, 1994. These numbers exist for only 1, 3, 4, 5, 6, 7, 8, 9, 10, 11, 14, 16, 17, 19, 20, 21, 23, 24, 25, 27, 29, 31, 32, 33, 34, 35, 37, 38, and 39 (OEIS A114904) digits, and the series of smallest narcissistic numbers of 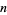 digits are 0, (none), 153, 1634, 54748, 548834, ... (OEIS A014576).
digits are 0, (none), 153, 1634, 54748, 548834, ... (OEIS A014576).
 |
base-10 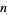 -narcissistic numbers -narcissistic numbers |
| 1 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| 3 | 153, 370, 371, 407 |
| 4 | 1634, 8208, 9474 |
| 5 | 54748, 92727, 93084 |
| 6 | 548834 |
| 7 | 1741725, 4210818, 9800817, 9926315 |
| 8 | 24678050, 24678051, 88593477 |
| 9 | 146511208, 472335975, 534494836, 912985153 |
| 10 | 4679307774 |
| 11 | 32164049650, 32164049651, 40028394225, 42678290603, 44708635679, 49388550606, 82693916578, 94204591914 |
| 14 | 28116440335967 |
| 16 | 4338281769391370, 4338281769391371 |
| 17 | 21897142587612075, 35641594208964132, 35875699062250035 |
| 19 | 1517841543307505039, 3289582984443187032, 4498128791164624869, 4929273885928088826 |
| 20 | 63105425988599693916 |
| 21 | 128468643043731391252, 449177399146038697307 |
| 23 | 21887696841122916288858, 27879694893054074471405, 27907865009977052567814, 28361281321319229463398, 35452590104031691935943 |
| 24 | 174088005938065293023722, 188451485447897896036875, 239313664430041569350093 |
| 25 | 1550475334214501539088894, 1553242162893771850669378, 3706907995955475988644380, 3706907995955475988644381, 4422095118095899619457938 |
| 27 | 121204998563613372405438066, 121270696006801314328439376, 128851796696487777842012787, 174650464499531377631639254, 177265453171792792366489765 |
| 29 | 14607640612971980372614873089, 19008174136254279995012734740, 19008174136254279995012734741, 23866716435523975980390369295 |
| 31 | 1145037275765491025924292050346, 1927890457142960697580636236639, 2309092682616190307509695338915 |
| 32 | 17333509997782249308725103962772 |
| 33 | 186709961001538790100634132976990, 186709961001538790100634132976991 |
| 34 | 1122763285329372541592822900204593 |
| 35 | 12639369517103790328947807201478392, 12679937780272278566303885594196922 |
| 37 | 1219167219625434121569735803609966019 |
| 38 | 12815792078366059955099770545296129367 |
| 39 | 115132219018763992565095597973971522400, 115132219018763992565095597973971522401 |
The table below gives the first few base-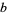 narcissistic numbers for small bases
narcissistic numbers for small bases 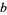 . A table of the largest known narcissistic numbers in various bases is given by Pickover (1995) and a tabulation of narcissistic numbers in various bases is given by Corning.
. A table of the largest known narcissistic numbers in various bases is given by Pickover (1995) and a tabulation of narcissistic numbers in various bases is given by Corning.
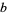 |
OEIS | base-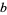 narcissistic numbers narcissistic numbers |
| 2 | 1 | |
| 3 | 1, 2, 5, 8, 17 | |
| 4 | A010344 | 1, 2, 3, 28, 29, 35, 43, 55, 62, 83, 243 |
| 5 | A010346 | 1, 2, 3, 4, 13, 18, 28, 118, 289, 353, 419, 4890, 4891, 9113 |
| 6 | A010348 | 1, 2, 3, 4, 5, 99, 190, 2292, 2293, 2324, 3432, 3433, 6197, ... |
| 7 | A010350 | 1, 2, 3, 4, 5, 6, 10, 25, 32, 45, 133, 134, 152, 250, 3190, ... |
| 8 | A010354 | 1, 2, 3, 4, 5, 6, 7, 20, 52, 92, 133, 307, 432, 433, ... |
| 9 | A010353 | 1, 2, 3, 4, 5, 6, 7, 8, 41, 50, 126, 127, 468, ... |
A closely related set of numbers generalize the narcissistic number to 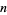 -digit numbers which are the sums of any single power of their digits. For example, 4150 is a 4-digit number which is the sum of fifth powers of its digits. Since the number of digits is not equal to the power to which they are taken for such numbers, they are not narcissistic numbers. The smallest numbers which are sums of any single positive power of their digits are 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407, 1634, 4150, 4151, 8208, 9474, ... (OEIS A023052), with powers 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 3, 3, 3, 4, 5, 5, 4, 4, ... (OEIS A046074).
-digit numbers which are the sums of any single power of their digits. For example, 4150 is a 4-digit number which is the sum of fifth powers of its digits. Since the number of digits is not equal to the power to which they are taken for such numbers, they are not narcissistic numbers. The smallest numbers which are sums of any single positive power of their digits are 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407, 1634, 4150, 4151, 8208, 9474, ... (OEIS A023052), with powers 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 3, 3, 3, 4, 5, 5, 4, 4, ... (OEIS A046074).
Another set of related numbers are the Münchhausen numbers, which are numbers equal to the sum of their digits raised to each digit's power.
The smallest numbers which are equal to the 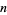 th powers of their digits for
th powers of their digits for 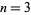 , 4, ..., are 153, 1634, 4150, 548834, 1741725, ... (OEIS A003321). The
, 4, ..., are 153, 1634, 4150, 548834, 1741725, ... (OEIS A003321). The 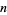 -digit numbers equal to the sum of
-digit numbers equal to the sum of 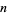 th powers of their digits (a finite sequence) are called Armstrong numbers or plus perfect number and are given by 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407, 1634, 8208, 9474, 54748, ... (OEIS A005188).
th powers of their digits (a finite sequence) are called Armstrong numbers or plus perfect number and are given by 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407, 1634, 8208, 9474, 54748, ... (OEIS A005188).
If the sum-of-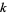 th-powers-of-digits operation applied iteratively to a number
th-powers-of-digits operation applied iteratively to a number 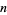 eventually returns to
eventually returns to 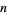 , the smallest number in the sequence is called a
, the smallest number in the sequence is called a 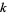 -recurring digital invariant.
-recurring digital invariant.
The numbers that are equal to the sum of consecutive powers of their digits are given by 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 89, 135, 175, 518, 598, 1306, 1676, 2427, 2646798 (OEIS A032799), e.g.,
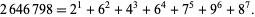 |
(3) |
The values obtained by summing the 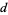 th powers of the digits of a
th powers of the digits of a 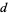 -digit number
-digit number 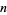 for
for 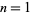 , 2, ... are 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 2, 5, 10, 17, 26, ... (OEIS A101337).
, 2, ... are 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 2, 5, 10, 17, 26, ... (OEIS A101337).
REFERENCES:
Corning, T. "Exponential Digital Invariants." https://members.aol.com/tec153/Edi4web/Edi.html
Deimel, L. E. Jr. and Jones, M. T. "Finding Pluperfect Digital Invariants: Techniques, Results and Observations." J. Recr. Math. 14, 97-108, 1981.
Hardy, G. H. A Mathematician's Apology. New York: Cambridge University Press, p. 105, 1993.
Heinz, H. "Narcissistic Numbers." https://www.magic-squares.net/narciss.htm.
Keith, M. "Wild Narcissistic Numbers." https://users.aol.com/s6sj7gt/mikewild.htm.
Lamoitier, J. P. "Fifty Basic Exercises." SYBEX Inc., 1981.
Madachy, J. S. "Narcissistic Numbers." Madachy's Mathematical Recreations. New York: Dover, pp. 163-173, 1979.
Pickover, C. A. Keys to Infinity. New York: Wiley, pp. 169-170, 1995.
Pickover, C. A. "The Latest Gossip on Narcissistic Numbers." Ch. 88 in Wonders of Numbers: Adventures in Mathematics, Mind, and Meaning. Oxford, England: Oxford University Press, pp. 204-205, 2001.
Rivera, C. "Problems & Puzzles: Puzzle 015-Narcissistic and Handsome Primes." https://www.primepuzzles.net/puzzles/puzz_015.htm.
Roberts, J. The Lure of the Integers. Washington, DC: Math. Assoc. Amer., p. 35, 1992.
Rumney, M. "Digital Invariants." Recr. Math. Mag. No. 12, 6-8, Dec. 1962.
Sloane, N. J. A. Sequences A005188/M0488, A003321/M5403, A010344, A010346, A010348, A010350, A010353, A010354, A014576, A023052, A032799, A046074, A101337, and A114904 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|