المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Mian-Chowla Sequence |
 718
 02:08 صباحاً
date: 2-11-2020 |
Author : Mian, A. M. and Chowla, S. D. 
Book or Source : "On the B_2-Sequences of Sidon." Proc. Nat. Acad. Sci. India A14 
Page and Part : ...|
Read More
Date: 17-3-2020
891
Date: 25-2-2020
665
Date: 24-1-2020
1226
|
The sequence produced by starting with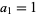 
and applying the greedy algorithm in the following way: for each 
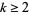, let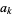 
be the least integer exceeding 
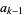for which 
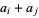are all distinct, with 
.
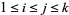This procedure generates the sequence 1, 2, 4, 8, 13, 21, 31, 45, 66, 81, 97, 123, 148, 182, 204, 252, 290, ... (OEIS A005282). The reciprocal sum of the sequence,
 |
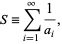satisfies
 |
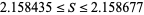(R. Lewis).
REFERENCES:
Mian, A. M. and Chowla, S. D. "On the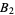 
-Sequences of Sidon." Proc. Nat. Acad. Sci. India A14, 3-4, 1944.
Guy, R. K. "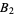
-Sequences." §E28 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 228-229, 1994.
Sloane, N. J. A. Sequence A005282/M1094 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|
