Magata,s Constant

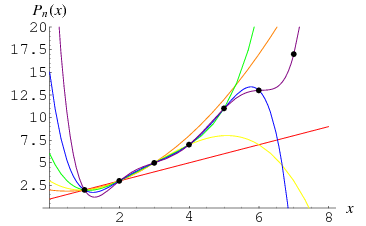
Consider the Lagrange interpolating polynomial

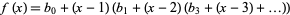(1)

through the points 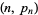, where  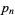is the 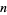th prime. For the first few points, the polynomials are

			(2)
			(3)
			(4)
			(5)
			(6)

So the first few values of 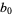, , 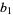, 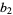..., are 2, 1, 1/2, 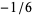, 1/8, 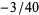, ... (OEIS A118210 and A118211).

Now consider the partial sums of these coefficients, namely 2, 3, 7/2, 10/3, 83/24, 203/60, 2459/720, ... (OEIS A118203 and A118204). As first noted by F. Magata in 1998, the sum appears to converge to the value 3.407069... (OEIS A092894), now known as Magata's constant.

REFERENCES:

Sloane, N. J. A. Sequences A092894, A118203, A118204, A118210, and A118210 in "The On-Line Encyclopedia of Integer Sequences."