المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Hofstadter Sequences |
 738
 03:27 مساءً
date: 28-10-2020 |
Author : Guy, R. K. 
Book or Source : "Three Sequences of Hofstadter." §E31 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag 
Page and Part : ...|
Read More
Date: 21-3-2020
538
Date: 8-10-2020
662
Date: 16-10-2019
535
|
Let 
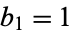and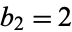 
and for 
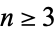, let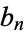 
be the least integer 
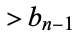which can be expressed as the sum of two or more consecutive terms. The resulting sequence is 1, 2, 3, 5, 6, 8, 10, 11, 14, 16, ... (OEIS A005243). Let 
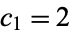and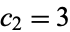 
, form all possible expressions of the form 
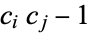for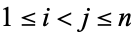 
, and append them. The resulting sequence is 2, 3, 5, 9, 14, 17, 26, 27, ... (OEIS A005244).
REFERENCES:
Guy, R. K. "Three Sequences of Hofstadter." §E31 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 231-232, 1994.
Sloane, N. J. A. Sequences A005243/M0623 and A005244/M0705 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
|
|
|
