Hofstadter-Conway $10,000 Sequence

The recursive sequence defined by the recurrence relation

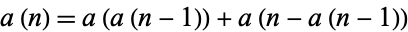(1)

with 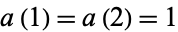. The first few values are 1, 1, 2, 2, 3, 4, 4, 4, 5, 6, ... (OEIS A004001; Wolfram 2002, pp. 129-130, sequence (c)). Conway (1988) showed that  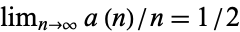and offered a prize of  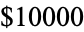to the discoverer of a value of  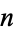for which  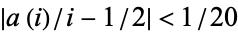for 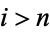. The prize was subsequently claimed by Mallows, after adjustment to Conway's "intended" prize of  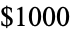(Schroeder 1991), who found .

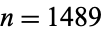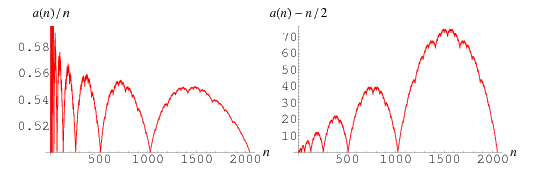
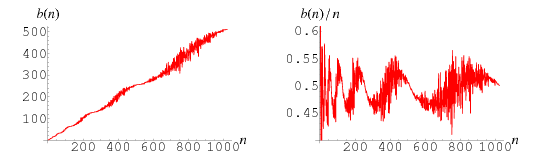
The plots above show 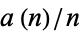 (left plot) and  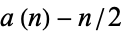(right plot). Amazingly,  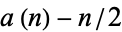reveals itself to consist of a series of increasingly larger versions of the batrachion Blancmange function.

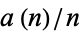 takes a value of 1/2 for  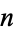of the form  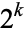with 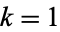, 2, .... More generally,

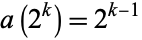(2)

and

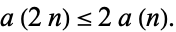(3)

Pickover (1995) gives a table of analogous values of 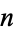 corresponding to different values of .

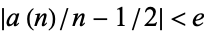A related chaotic sequence is given by the recurrence equation

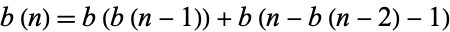(4)

with 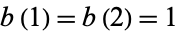, which gives the sequence 1, 1, 2, 2, 2, 3, 4, 4, 4, 4, 5, 6, 7, 8, 8, 8, 8, 8, 8, ... (OEIS A055748; Pinn 2000; Wolfram 2002, pp. 129-130, sequence (g)).

REFERENCES:

Bloom, D. M. "Newman-Conway Sequence." Solution to Problem 1459. Math. Mag. 68, 400-401, 1995.

Conolly, B. W. "Meta-Fibonacci Sequences." In Fibonacci and Lucas Numbers, and the Golden Section (Ed. S. Vajda). New York: Halstead Press, pp. 127-138, 1989.

Conway, J. "Some Crazy Sequences." Lecture at AT&T Bell Labs, July 15, 1988.

Guy, R. K. "Three Sequences of Hofstadter." §E31 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 231-232, 1994.

Kubo, T. and Vakil, R. "On Conway's Recursive Sequence." Disc. Math. 152, 225-252, 1996.

Mallows, C. L. "Conway's Challenge Sequence." Amer. Math. Monthly 98, 5-20, 1991.

Pickover, C. A. "The Drums of Ulupu." In Mazes for the Mind: Computers and the Unexpected. New York: St. Martin's Press, 1993.

Pickover, C. A. "The Crying of Fractal Batrachion ." Ch. 25 in Keys to Infinity. New York: W. H. Freeman, pp. 183-191, 1995.

Pickover, C. A. "The Crying of Fractal Batrachion ." Comput. & Graphics 19, 611-615, 1995. Reprinted in Chaos and Fractals, A Computer Graphical Journey: Ten Year Compilation of Advanced Research (Ed. C. A. Pickover). Amsterdam, Netherlands: Elsevier, pp. 127-131, 1998.

Pinn, K. "A Chaotic Cousin of Conway's Recursive Sequence." Exp. Math. 9, 55-66, 2000.

Schroeder, M. "John Horton Conway's 'Death Bet.' " Fractals, Chaos, Power Laws. New York: W. H. Freeman, pp. 57-59, 1991.

Sloane, N. J. A. Sequences A004001/M0276 and A055748 in "The On-Line Encyclopedia of Integer Sequences."

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, pp. 129-130, 2002.