Fractal Sequence
المؤلف:
Kimberling, C.
المصدر:
"Fractal Sequences and Interspersions." Ars Combin. 45
الجزء والصفحة:
157-168
27-10-2020
962
Fractal Sequence
Given an infinitive sequence ![<span style=]()
{x_n}" src="https://mathworld.wolfram.com/images/equations/FractalSequence/Inline1.gif" style="height:15px; width:23px" /> with associative array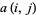 
, then ![<span style=]()
{x_n}" src="https://mathworld.wolfram.com/images/equations/FractalSequence/Inline3.gif" style="height:15px; width:23px" /> is said to be a fractal sequence
1. If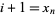 
, then there exists 
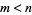such that 
,
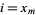2. If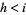 
, then, for every 
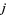, there is exactly one 
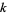such that 
.
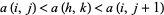(As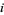 
and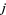 
range through 
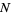, the array 
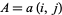, called the associative array of 
, ranges through all of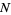 
.) An example of a fractal sequence is 1, 1, 1, 1, 2, 1, 2, 1, 3, 2, 1, 3, 2, 1, 3, ....
If ![<span style=]()
{x_n}" src="https://mathworld.wolfram.com/images/equations/FractalSequence/Inline17.gif" style="height:15px; width:23px" /> is a fractal sequence, then the associated array is an interspersion. If 
is a fractal sequence, then the upper-trimmed subsequence is given by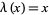 
, and the lower-trimmed subsequence 
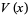is another fractal sequence. The signature of an irrational number is a fractal sequence.
REFERENCES:
Kimberling, C. "Fractal Sequences and Interspersions." Ars Combin. 45, 157-168, 1997.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
