


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 17-2-2020
Date: 23-10-2019
Date: 20-2-2020
|
There are (at least) three types of Euler transforms (or transformations). The first is a set of transformations of hypergeometric functions, called Euler's hypergeometric transformations.
The second type of Euler transform is a technique for series convergence improvement which takes a convergent alternating series
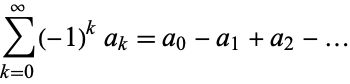 |
(1) |
into a series with more rapid convergence to the same value to
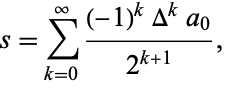 |
(2) |
where the forward difference is defined by
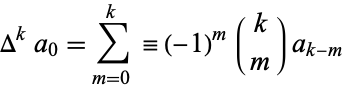 |
(3) |
(Abramowitz and Stegun 1972; Beeler et al. 1972). Euler's hypergeometric and convergence improvement transformations are related by the fact that when 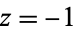 is taken in the second of Euler's hypergeometric transformations
is taken in the second of Euler's hypergeometric transformations
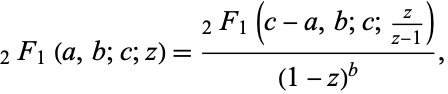 |
(4) |
where 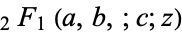 is a hypergeometric function, it gives Euler's convergence improvement transformation of the series
is a hypergeometric function, it gives Euler's convergence improvement transformation of the series 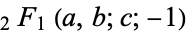 (Abramowitz and Stegun 1972, p. 555).
(Abramowitz and Stegun 1972, p. 555).
The third type of Euler transform is a relationship between certain types of integer sequences (Sloane and Plouffe 1995, pp. 20-21). If 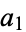 ,
, 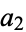 , ... and
, ... and 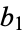 ,
, 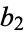 , ... are related by
, ... are related by
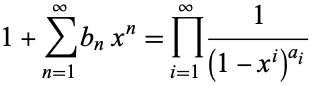 |
(5) |
or, in terms of generating functions 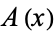 and
and 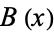 ,
,
![1+B(x)=exp[sum_(k=1)^infty(A(x^k))/k],](https://mathworld.wolfram.com/images/equations/EulerTransform/NumberedEquation6.gif) |
(6) |
then 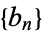 is said to be the Euler transform of
is said to be the Euler transform of 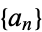 (Sloane and Plouffe 1995, p. 20). The Euler transform can be effected by introducing the intermediate series
(Sloane and Plouffe 1995, p. 20). The Euler transform can be effected by introducing the intermediate series 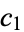 ,
, 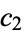 , ... given by
, ... given by
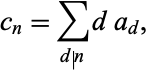 |
(7) |
then
![b_n=1/n[c_n+sum_(k=1)^(n-1)c_kb_(n-k)],](https://mathworld.wolfram.com/images/equations/EulerTransform/NumberedEquation8.gif) |
(8) |
with 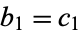 . Similarly, the inverse transform can be effected by computing the intermediate series as
. Similarly, the inverse transform can be effected by computing the intermediate series as
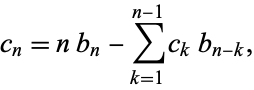 |
(9) |
then
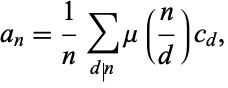 |
(10) |
where 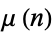 is the Möbius function.
is the Möbius function.
In graph theory, if 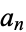 is the number of unlabeled connected graphs on
is the number of unlabeled connected graphs on 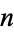 nodes satisfying some property, then
nodes satisfying some property, then 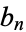 is the total number of unlabeled graphs (connected or not) with the same property. This application of the Euler transform is called Riddell's formula for unlabeled graph (Sloane and Plouffe 1995, p. 20).
is the total number of unlabeled graphs (connected or not) with the same property. This application of the Euler transform is called Riddell's formula for unlabeled graph (Sloane and Plouffe 1995, p. 20).
There are also important number theoretic applications of the Euler transform. For example, if there are 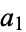 kinds of parts of size 1,
kinds of parts of size 1, 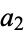 kinds of parts of size 2, etc., in a given type of partition, then the Euler transform
kinds of parts of size 2, etc., in a given type of partition, then the Euler transform 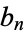 of
of 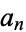 is the number of partitions of
is the number of partitions of 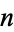 into these integer parts. For example, if
into these integer parts. For example, if 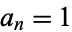 for all
for all 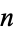 , then
, then 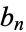 is the number of partitions of
is the number of partitions of 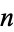 into integer parts. Similarly, if
into integer parts. Similarly, if 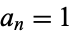 for
for 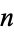 prime and
prime and 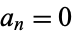 for
for 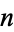 composite, then
composite, then 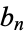 is the number of partitions of
is the number of partitions of 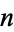 into prime parts (Sloane and Plouffe 1995, p. 21). Other applications are given by Andrews (1986), Andrews and Baxter (1989), and Cameron (1989).
into prime parts (Sloane and Plouffe 1995, p. 21). Other applications are given by Andrews (1986), Andrews and Baxter (1989), and Cameron (1989).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 16, 1972.
Andrews, G. E. q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math. Soc., 1986.
Andrews, G. E. and Baxter, R. J. "A Motivated Proof of the Rogers-Ramanujan Identities." Amer. Math. Monthly 96, 401-409, 1989.
Beeler, M. et al. Item 120 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 55, Feb. 1972. https://www.inwap.com/pdp10/hbaker/hakmem/series.html#item120.
Bernstein, M. and Sloane, N. J. A. "Some Canonical Sequences of Integers." Linear Algebra Appl. 226//228, 57-72, 1995.
Cameron, P. J. "Some Sequences of Integers." Disc. Math. 75, 89-102, 1989.
Iyanaga, S. and Kawada, Y. (Eds.). Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1163, 1980.
Sloane, N. J. A. and Plouffe, S. The Encyclopedia of Integer Sequences. San Diego, CA: Academic Press, pp. 20-21, 1995.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|