
Binomial Transform
 المؤلف:
Bernstein, M. and Sloane, N. J. A.
المؤلف:
Bernstein, M. and Sloane, N. J. A.
 المصدر:
"Some Canonical Sequences of Integers." Linear Algebra Appl. 226/228
المصدر:
"Some Canonical Sequences of Integers." Linear Algebra Appl. 226/228
 الجزء والصفحة:
...
الجزء والصفحة:
...
 24-10-2020
24-10-2020
 1186
1186
Binomial Transform
The binomial transform takes the sequence 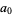 ,
, 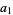 ,
, 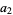 , ... to the sequence
, ... to the sequence 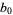 ,
, 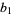 ,
, 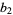 , ... via the transformation
, ... via the transformation
The inverse transform is
(Sloane and Plouffe 1995, pp. 13 and 22). The inverse binomial transform of 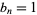 for prime
for prime 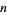 and
and 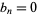 for composite
for composite 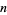 is 0, 1, 3, 6, 11, 20, 37, 70, ... (OEIS A052467). The inverse binomial transform of
is 0, 1, 3, 6, 11, 20, 37, 70, ... (OEIS A052467). The inverse binomial transform of 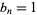 for even
for even 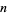 and
and 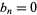 for odd
for odd 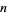 is 0, 1, 2, 4, 8, 16, 32, 64, ... (OEIS A000079). Similarly, the inverse binomial transform of
is 0, 1, 2, 4, 8, 16, 32, 64, ... (OEIS A000079). Similarly, the inverse binomial transform of 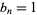 for odd
for odd 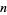 and
and 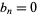 for even
for even 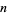 is 1, 2, 4, 8, 16, 32, 64, ... (OEIS A000079). The inverse binomial transform of the Bell numbers 1, 1, 2, 5, 15, 52, 203, ... (OEIS A000110) is a shifted version of the same numbers: 1, 2, 5, 15, 52, 203, ... (Bernstein and Sloane 1995, Sloane and Plouffe 1995, p. 22).
is 1, 2, 4, 8, 16, 32, 64, ... (OEIS A000079). The inverse binomial transform of the Bell numbers 1, 1, 2, 5, 15, 52, 203, ... (OEIS A000110) is a shifted version of the same numbers: 1, 2, 5, 15, 52, 203, ... (Bernstein and Sloane 1995, Sloane and Plouffe 1995, p. 22).
The central and raw moments of statistical distributions are also related by the binomial transform.
REFERENCES:
Bernstein, M. and Sloane, N. J. A. "Some Canonical Sequences of Integers." Linear Algebra Appl. 226/228, 57-72, 1995.
Sloane, N. J. A. Sequences A000079/M1129, A000110/M1484, and A052467 in "The On-Line Encyclopedia of Integer Sequences."
Sloane, N. J. A. and Plouffe, S. The Encyclopedia of Integer Sequences. San Diego, CA: Academic Press, 1995.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


