A 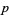-adic number is an extension of the field of rationals such that congruences modulo powers of a fixed prime  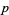are related to proximity in the so called "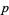-adic metric."

Any nonzero rational number  can be represented by

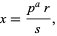(1)

where 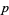 is a prime number,  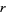and 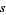 are integers not divisible by 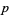, and 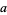 is a unique integer. Then define the p-adic norm of  by

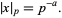(2)

Also define the 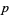-adic norm

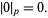(3)

The 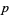-adics were probably first introduced by Hensel (1897) in a paper which was concerned with the development of algebraic numbers in power series. 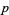-adic numbers were then generalized to valuations by Kűrschák in 1913. Hasse (1923) subsequently formulated the Hasse principle, which is one of the chief applications of local field theory. Skolem's 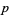-adic method, which is used in attacking certain Diophantine equations, is another powerful application of 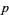-adic numbers. Another application is the theorem that the harmonic numbers  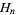are never integers (except for 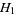). A similar application is the proof of the von Staudt-Clausen theorem using the 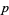-adic valuation, although the technical details are somewhat difficult. Yet another application is provided by the Mahler-Lech theorem.

Every rational  has an "essentially" unique 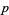-adic expansion ("essentially" since zero terms can always be added at the beginning)

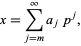(4)

with 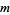 an integer,  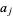the integers between 0 and  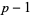inclusive, and where the sum is convergent with respect to 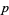-adic valuation. If  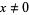and 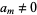, then the expansion is unique. Burger and Struppeck (1996) show that for  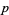a prime and  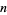a positive integer,

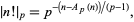(5)

where the 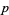-adic expansion of  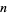is

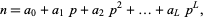(6)

and

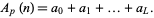(7)

For sufficiently large ,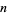

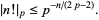(8)

The 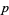-adic valuation on  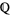gives rise to the 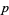-adic metric

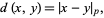(9)

which in turn gives rise to the 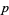-adic topology. It can be shown that the rationals, together with the 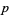-adic metric, do not form a complete metric space. The completion of this space can therefore be constructed, and the set of 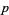-adic numbers  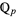is defined to be this completed space.

Just as the real numbers are the completion of the rationals 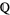 with respect to the usual absolute valuation 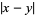, the 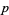-adic numbers are the completion of  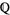with respect to the 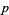-adic valuation 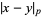. The 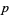-adic numbers are useful in solving Diophantine equations. For example, the equation  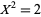can easily be shown to have no solutions in the field of 2-adic numbers (we simply take the valuation of both sides). Because the 2-adic numbers contain the rationals as a subset, we can immediately see that the equation has no solutions in the rationals. So we have an immediate proof of the irrationality of .

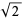This is a common argument that is used in solving these types of equations: in order to show that an equation has no solutions in 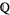, we show that it has no solutions in an extension field. For another example, consider 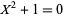. This equation has no solutions in  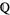because it has no solutions in the reals 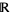, and 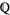 is a subset of .

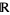Now consider the converse. Suppose we have an equation that does have solutions in 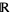 and in all the  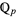for every prime 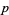. Can we conclude that the equation has a solution in 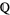? Unfortunately, in general, the answer is no, but there are classes of equations for which the answer is yes. Such equations are said to satisfy the Hasse principle.

REFERENCES:

Burger, E. B. and Struppeck, T. "Does 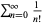 Really Converge? Infinite Series and p-adic Analysis." Amer. Math. Monthly 103, 565-577, 1996.

Cassels, J. W. S. Ch. 2 in Lectures on Elliptic Curves. New York: Cambridge University Press, 1991.

Cassels, J. W. S. and Scott, J. W. Local Fields. Cambridge, England: Cambridge University Press, 1986.

De Smedt, S. "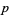-adic Arithmetic." The Mathematica J. 9, 349-357, 2004.

Gouvêa, F. Q. P-adic Numbers: An Introduction, 2nd ed. New York: Springer-Verlag, 1997.

Hasse, H. "Über die Darstellbarkeit von Zahlen durch quadratische Formen im Körper der rationalen Zahlen." J. reine angew. Math. 152, 129-148, 1923.

Hasse, H. "Die Normenresttheorie relativ-Abelscher Zahlkörper als Klassenkörpertheorie in Kleinen." J. reine angew. Math. 162, 145-154, 1930.

Hensel, K. "Über eine neue Begründung der Theorie der algebraischen Zahlen." Jahresber. Deutsch. Math. Verein 6, 83-88, 1897.

Kakol, J.; De Grande-De Kimpe, N.; and Perez-Garcia, C. (Eds.). p-adic Functional Analysis. New York: Dekker, 1999.

Koblitz, N. P-adic Numbers, P-adic Analysis, and Zeta-Functions, 2nd ed. New York: Springer-Verlag, 1984.

Koch, H. "Valuations." Ch. 4 in Number Theory: Algebraic Numbers and Functions. Providence, RI: Amer. Math. Soc., pp. 103-139, 2000.

Mahler, K. P-adic Numbers and Their Functions, 2nd ed. Cambridge, England: Cambridge University Press, 1981.

Ostrowski, A. "Über sogennante perfekte Körper." J. reine angew. Math. 147, 191-204, 1917.

Vladimirov, V. S. "Tables of Integrals of Complex-Valued Functions of p.-adic Arguments" 22 Nov 1999. https://arxiv.org/abs/math-ph/9911027.

Weisstein, E. W. "Books about P-adic Numbers." https://www.ericweisstein.com/encyclopedias/books/P-adicNumbers.html.

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 1168, 2002.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الشؤون الطبية يقدم الخدمات الصحية والعلاجية لزائري مدينة سامراء

العتبة العباسية المقدسة تقدم خدماتها لزائري مرقد الإمامين العسكريين (عليهما السلام) في سامراء

المجمَع العلمي ووفد وزارة التربية يبحثان سبل التعاون المشترك

قسم الشؤون الفكرية يصدر العدد 192 من مجلة الرياحين للأطفال

المزيد

الآخبار الصحية

كنز غذائي على طبقك.. ماذا تفعل السبانخ بجسمك؟

ما لا يتوقعه أحد.. "سر غذائي" في الجبن الدسم

لتحسين الهضم والنوم.. هذا أفضل وقت لتناول العشاء

10 طرق بسيطة وغير مألوفة لحرق المزيد من السعرات يوميا

المزيد

الآخبار التكنلوجية

سابقة بعالم الطيران.. طائرة تقرر الهبوط بنفسها بعد ظرف طارئ

"الإنفلونزا الخارقة" تكتسح دول العالم.. وتثير قلقا كبيرا

مرحلة ما قبل الأعراض.. دواء جديد يستهدف "شرارة" الزهايمر

إزالة ثاني أكسيد الكربون من الغلاف الجوي.. ما دور المحيطات والبحار؟

المزيد