المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Heath-Brown-Moroz Constant |
 831
 04:32 مساءً
date: 3-10-2020 |
Author : Finch, S. R 
Book or Source : Mathematical Constants. Cambridge, England: Cambridge University Press 
Page and Part : ...|
Read More
Date: 8-5-2020
832
Date: 30-11-2020
800
Date: 19-12-2019
1005
|
The Heath-Brown-Moroz constant is defined by
 |
 |
 |
(1) |
 |
 |
 |
(2) |
(OEIS A118228), where the product is taken over the primes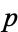 
.
REFERENCES:
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, p. 106, 2003.
Heath-Brown, D. R. and Moroz, B. Z. "The Density of Rational Points on the Cubic Surface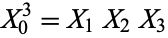 
." Math. Proc. Cambridge Philos. Soc. 125, 385-395, 1999.
Niklasch, G. "Some Number-Theoretical Constants." https://www.gn-50uma.de/alula/essays/Moree/Moree.en.shtml.
Sloane, N. J. A. Sequence A118228 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقدم دعوة إلى كلية مزايا الجامعة للمشاركة في حفل التخرج المركزي الخامس
|
|
|
