


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-1-2020
Date: 19-8-2020
Date: 11-6-2020
|
The tribonacci numbers are a generalization of the Fibonacci numbers defined by 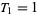 ,
, 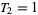 ,
, 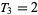 , and the recurrence equation
, and the recurrence equation
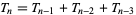 |
(1) |
for 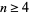 (e.g., Develin 2000). They represent the
(e.g., Develin 2000). They represent the 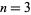 case of the Fibonacci n-step numbers.
case of the Fibonacci n-step numbers.
The first few terms using the above indexing convention for 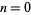 , 1, 2, ... are 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, ... (OEIS A000073; which however adopts the alternate indexing convention
, 1, 2, ... are 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, ... (OEIS A000073; which however adopts the alternate indexing convention 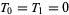 and
and 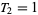 ).
).
The first few prime tribonacci numbers are 2, 7, 13, 149, 19341322569415713958901, ... (OEIS A092836), which have indices 3, 5, 6, 10, 86, 97, 214, 801, 4201, 18698, 96878, ... (OEIS A092835), and no others with 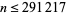 (E. W. Weisstein, Mar. 21, 2009).
(E. W. Weisstein, Mar. 21, 2009).
Using Brown's criterion, it can be shown that the tribonacci numbers are complete; that is, every positive number can be written as the sum of distinct tribonacci numbers. Moreover, every positive number has a unique Zeckendorf-like expansion as the sum of distinct tribonacci numbers and that sum does not contain three consecutive tribonacci numbers. The Zeckendorf-like expansion can be computed using a greedy algorithm.
An exact expression for the 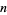 th tribonacci number can be given explicitly by
th tribonacci number can be given explicitly by
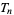 |
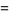 |
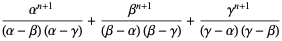 |
(2) |
 |
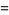 |
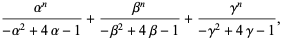 |
(3) |
where 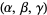 are the three roots of the polynomial
are the three roots of the polynomial
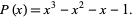 |
(4) |
This can be written in slightly more concise form as
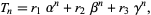 |
(5) |
where 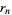 is the
is the 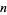 th root of the polynomial
th root of the polynomial
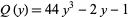 |
(6) |
and 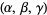 and
and 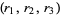 are in the ordering of the Wolfram Language's Root object.
are in the ordering of the Wolfram Language's Root object.
The tribonacci numbers can also be computed using the generating function
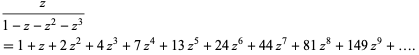 |
(7) |
Another explicit formula for 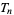 is also given by
is also given by
![[3({1/3(19+3sqrt(33))^(1/3)+1/3(19-3sqrt(33))^(1/3)+1/3}^n(586+102sqrt(33))^(1/3))/((586+102sqrt(33))^(2/3)+4-2(586+102sqrt(33))^(1/3))],](https://mathworld.wolfram.com/images/equations/TribonacciNumber/NumberedEquation6.gif) |
(8) |
where ![[x]](https://mathworld.wolfram.com/images/equations/TribonacciNumber/Inline23.gif) denotes the nearest integer function (Plouffe). The first part of the numerator is related to the real root of
denotes the nearest integer function (Plouffe). The first part of the numerator is related to the real root of 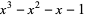 , but determination of the denominator requires an application of the LLL algorithm.
, but determination of the denominator requires an application of the LLL algorithm.
The ratio of adjacent terms tends to the positive real root 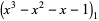 , namely 1.83929... (OEIS A058265), sometimes known as the tribonacci constant.
, namely 1.83929... (OEIS A058265), sometimes known as the tribonacci constant.
By considering the series 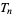 (mod
(mod 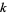 ), one can prove that any integer
), one can prove that any integer 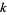 is a factor of
is a factor of 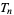 for some
for some 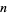 (Brenner 1954). The smallest values of
(Brenner 1954). The smallest values of 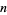 for which
for which 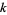 is a factor for
is a factor for 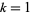 , 2, ... are given by 1, 3, 7, 4, 14, 7, 5, 7, 9, 19, 8, 7, 6, ... (OEIS A112305).
, 2, ... are given by 1, 3, 7, 4, 14, 7, 5, 7, 9, 19, 8, 7, 6, ... (OEIS A112305).
The tribonacci constant is extremely prominent in the properties of the snub cube, its dual the pentagonal icositetrahedron, and the snub cube-pentagonal icositetrahedron compound. It can even be used to express the hard hexagon entropy constant.
With different initial values, the tribonacci sequence starts as 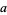 ,
, 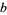 ,
, 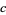 ,
, 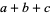 ,
, 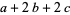 ,
, 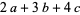 ,
, 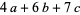 ,
, 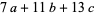 , ..., which gives the following sequences as special cases.
, ..., which gives the following sequences as special cases.
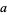 |
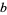 |
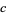 |
OEIS | sequence |
| 0 | 0 | 1 | A000073 | 0, 1, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, ... |
| 1 | 1 | 1 | A000213 | 1, 1, 1, 3, 5, 9, 17, 31, 57, 105, 193, 355, ... |
| 0 | 1 | 0 | A001590 | 0, 1, 0, 1, 2, 3, 6, 11, 20, 37, 68, 125, 230, ... |
| 3 | 1 | 3 | A001644 | 3, 1, 3, 7, 11, 21, 39, 71, 131, 241, 443, 815, ... |
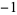 |
2 | 2 | A100683 | 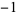 , 2, 2, 3, 7, 12, 22, 41, 75, 138, 254, 467, ... , 2, 2, 3, 7, 12, 22, 41, 75, 138, 254, 467, ... |
REFERENCES:
Brenner, J. L. "Linear Recurrence Relations." Amer. Math. Monthly 61, 171-173, 1954.
Develin, M. "A Complete Categorization of When Generalized Tribonacci Sequences Can Be Avoided by Additive Partitions." Electronic J. Combinatorics 7, No. 1, R53, 1-7, 2000. https://www.combinatorics.org/Volume_7/Abstracts/v7i1r53.html.
Dumitriu, I. "On Generalized Tribonacci Sequences and Additive Partitions." Disc. Math. 219, 65-83, 2000.
Feinberg, M. "Fibonacci-Tribonacci." Fib. Quart. 1, 71-74, 1963.
Hoggatt, V. E. Jr. "Additive Partitions of the Positive Integers." Fib. Quart. 18, 220-226, 1980.
Plouffe, S. "The Tribonacci Constant." https://pi.lacim.uqam.ca/piDATA/tribo.txt.
Sloane, N. J. A. Sequences A000073/M1074, A000213/M2454, A001590/M0784, A001644/M2625, A058265, A092835, A092836, A100683,and A112305 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
ضمن أسبوع الإرشاد النفسي.. جامعة العميد تُقيم أنشطةً ثقافية وتطويرية لطلبتها
|
|
|