Near-Square Prime

Call a number of the form 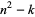 a "near-square number."

Numbers of the form 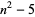 for 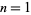, 2, ... are 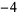, , 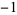4, 11, 20, 31, 44, 59, 76, 95, ... (OEIS A028875). These are prime for indices 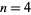, 6, 8, 12, 14, 16, ... (OEIS A028876), corresponding to the primes 11, 31, 59, 139, 191, 251, 479, ... (OEIS A028877).

Numbers of the form 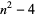 for 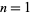, 2, ... are 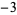, 0, 5, 12, 21, 32, 45, 60, ... (OEIS A028347). Since they can always be factored as  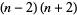for 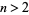, the only (positive) prime of this form is 5.

Numbers of the form 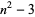 for 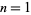, 2, ... are 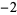, 1, 6, 13, 22, 33, 46, 61, ... (OEIS A028872). These are prime for indices 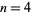, 8, 10, 14, 20, 26, 32, ... (OEIS A028873), corresponding to the primes 13, 61, 97, 193, 397, 673, ... (OEIS A028874).

Numbers of the form 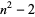 for 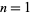, 2, ... are 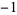, 2, 7, 14, 23, 34, 47, 62, ... (OEIS A008865). These are prime for indices 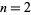, 3, 5, 7, 9, 13, 15, 19, 21, 27, ... (OEIS A028870), corresponding to the primes 2, 7, 23, 47, 79, 167, 223, 359, 439, ... (OEIS A028871). The "Kynea primes" (see below) are special cases of this form.

Numbers of the form 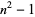 for 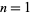, 2, ... are 0, 3, 8, 15, 24, 35, 48, 63, ... (OEIS A005563). Since they can always be factored as  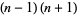for 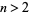, the only prime of this form is 3.

Numbers of the form 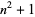 for 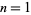, 2, ... are 2, 5, 10, 17, 26, 37, 50, ... (OEIS A002522). These are prime for indices 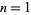, 2, 4, 6, 10, 14, 16, 20, 24, 26, 36, ... (OEIS A005574), corresponding to the primes 2, 5, 17, 37, 101, 197, 257, 401, 577, 677, ... (OEIS A002496). Fermat primes and generalized Fermat primes (with 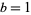) are of this form.

Numbers of the form 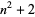 for 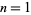, 2, ... are 3, 6, 11, 18, 27, 38, 51, 66, 83, 102, ... (OEIS A059100). These are prime for indices 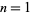, 3, 9, 15, 21, 33, 39, 45, 57, 81, 99, ... (OEIS A067201), corresponding to the primes 3, 11, 83, 227, 443, 1091, 1523, 2027, ... (OEIS A056899).

Numbers of the form 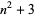 for 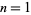, 2, ... are 4, 7, 12, 19, 28, 39, 52, 67, ... (OEIS A117950). These are prime for indices 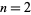, 4, 8, 10, 14, 22, 28, 38, 50, 52, 62, ... (OEIS A049422), corresponding to the primes 7, 19, 67, 103, 199, 487, 787, 1447, ... (OEIS A049423).

Numbers of the form 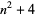 for 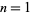, 2, ... are 5, 8, 13, 20, 29, 40, 53, 68, 85, ... (OEIS A087475). These are prime for indices 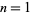, 3, 5, 7, 13, 15, 17, 27, ... (OEIS A007591), corresponding to the primes 5, 13, 29, 53, 173, 229, 293, 733, ... (OEIS A005473).

Numbers of the form 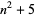 for 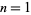, 2, ... are 6, 9, 14, 21, 30, 41, 54, 69, ... (OEIS A117951). These are prime for indices 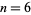, 12, 36, 48, 72, 78, 96, ... (OEIS A078402), corresponding to the primes 41, 149, 1301, 2309, 5189, ... (OEIS A056905).

For 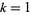, 2, ..., the first few near-square numbers of the form  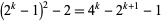are 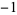, 7, 47, 223, 959, 3967, ... (OEIS A093112). As of Jun. 2016, a total of 42 primes of this form (arbitrarily dubbed Carol primes by their original investigator in reference to a personal acquaintance) are known. The first few have indices 2, 3, 4, 6, 7, 10, 12, 15, 18, 19, 21, 25, 27, 55, 129, ... (OEIS A091515), corresponding to the primes 7, 47, 223, 3967, 16127, 1046527, ... (OEIS A091516). Some large primes of this form are summarized in the following table.

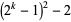	decimal digits	discoverer
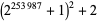	152916	C. Emmanuel (May 7, 2007; Harvey; https://primes.utm.edu/primes/page.php?id=80384)
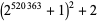	313290	M. Rodenkirch (Apr. 14, 2016)
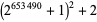	393441	M. Rodenkirch (Jun. 15, 2016)

For 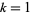, 2, ..., the first few near-square numbers of the form  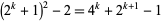are 2, 7, 23, 79, 287, 1087, 4223, 16639, ... (OEIS A093069). As of Jun. 2016, a total of 50 primes of this form (arbitrarily dubbed Kynea primes by their original investigator in reference to a personal acquaintance) are known. The first few have indices 0, 1, 2, 3, 5, 8, 9, 12, 15, 17, 18, 21, ... (OEIS A091513) and are given by 2, 7, 23, 79, 1087, 66047, 263167, 16785407, ... (OEIS A091514). Some large primes of this form are summarized in the following table.

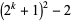	decimal digits	discoverer
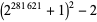	169553	C. Emmanuel (October 2005); https://primes.utm.edu/primes/page.php?id=75878
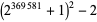	222510	M. Rodenkirch (Feb. 2016)
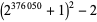	226405	M. Rodenkirch (Feb. 7, 2016)
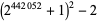	266142	M. Rodenkirch (Feb. 28, 2016)
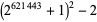	374146	M. Rodenkirch (May 30, 2016)
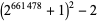	398250	M. Rodenkirch (Jun. 19, 2016)

REFERENCES:

Harvey, S. https://harvey563.tripod.com/Carol_Kynea.txt.

Minovic, P. "Carol/Kynea New Records." primenumbers discussion group. Feb. 20, 2004a. https://groups.yahoo.com/group/primenumbers/message/14574.

Minovic, P. "Re: Carol/Kynea New Records." primenumbers discussion group. Feb. 24, 2004b. https://groups.yahoo.com/group/primenumbers/message/14586.

Rodenkirch, M. "Carol and Kynea Prime Search." https://www.mersenneforum.org/rogue/ckps.html.

Sloane, N. J. A. Sequences A002496/M1506, A002522, A005563/M2720, A005574/M1010, A005473/M005473, A007591/M2416, A008865, A028347, A028870, A028871, A028872, A028873, A028874, A028875, A028876, A028877, A049422, A049423, A056899, A056905, A059100, A060867, A067201, A078402, A087475, A091513, A091514, A091515, A091516, A093069, A093112, A117950, and A117951 in "The On-Line Encyclopedia of Integer Sequences."