There exist a variety of formulas for either producing the 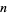th prime as a function of  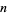or taking on only prime values. However, all such formulas require either extremely accurate knowledge of some unknown constant, or effectively require knowledge of the primes ahead of time in order to use the formula (Dudley 1969; Ribenboim 1996, p. 186). There also exist simple prime-generating polynomials that generate only primes for the first (possibly large) number of integer values.

There are also many beautiful formulas involving prime sums and prime products that can be done in closed form.

Considering examples of formulas that produce only prime numbers (although not necessarily the complete set of prime numbers ), there exists a constant 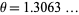 (OEIS A051021) known as Mills' constant such that

(1)

where 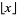 is the floor function, is prime for all  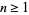(Ribenboim 1996, p. 186). The first few values of  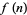are 2, 11, 1361, 2521008887, ... (OEIS A051254). It is not known if  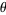is irrational. There also exists a constant  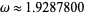(OEIS A086238) such that

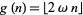(2)

(Wright 1951; Ribenboim 1996, p. 186) is prime for every 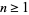. The first few values of  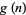are 3, 13, 16381, ... (OEIS A016104). In the case of both  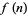and 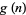, the numbers at  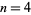grow so rapidly that an extremely precise value of  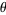or 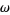 is needed in order to obtain the correct value, and values for  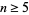are effectively incomputable.

Explicit formulas exist for the 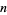th prime both as a function of  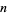and in terms of the primes 2, ...,  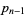(Hardy and Wright 1979, pp. 5-6, 344-345, and 414; Guy 1994, pp. 36-41), a number of which are given below. However, it should again be emphasized that these formulas are extremely inefficient, and in many (if not all) cases, simply performing an efficient sieving would yield the primes much more quickly and efficiently.

Let

			(3)
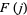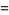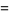		{1 for j=1 or j prime; 0 otherwise" src="https://mathworld.wolfram.com/images/equations/PrimeFormulas/Inline26.gif" style="height:41px; width:136px" />	(4)

for 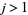 an integer, where  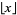is again the floor function. This formula is a consequence of Wilson's theorem and conceals the prime numbers  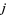as those for which 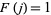, i.e., the values of  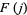are 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, ... (OEIS A080339). Then

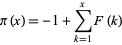(5)

and

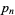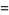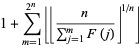			(6)
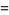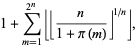			(7)

where 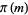 is the prime counting function (Willans 1964; Havil 2003, pp. 168-169).

Gandhi gave the formula in which 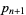 is the unique integer such that

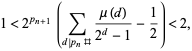(8)

where 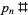 is the primorial function (Gandhi 1971, Eynden 1972, Golomb 1974) and  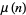is the Möbius function. It is also true that

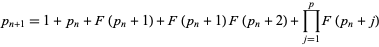(9)

(Ribenboim 1996, pp. 180-182). Note that the number of terms in the summation to obtain the 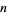th prime is 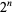, so these formulas turn out not to be practical in the study of primes.

Hardy and Wright (1979, p. 414) give the formula

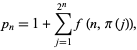(10)

for 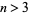, where

{0 for x=y; 1/2[1+(x-y)/(|x-y|)] for x!=y " src="https://mathworld.wolfram.com/images/equations/PrimeFormulas/NumberedEquation7.gif" style="height:64px; width:223px" />

(11)

and an "elementary" formula for the prime counting function is given by

(12)

(correcting a sign error), where 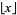 is the floor function.

A double sum for the 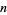th prime  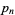is

(13)

where

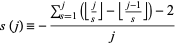(14)

(Ruiz 2000).

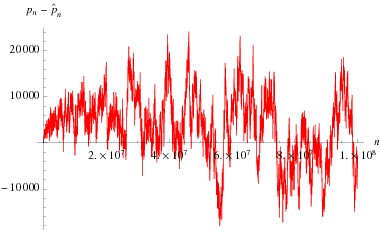
An asymptotic formula for 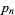 is given by

(15)

(Cipolla 1902). This asymptotic expansion is the inverse of the logarithmic integral 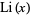 obtained by series reversion, where the inversion of  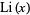gives 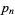 because the prime number theorem says that 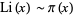, where  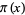is the prime counting function and the inverse of  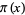is 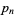 in the sense that 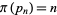. However, the formula oscillates a great deal as illustrated above, where  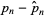is the difference between the actual 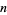th prime and that given by the Cipolla formula. Interestingly, truncating at  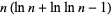gives the refined form of Rosser's theorem, which is a strict inequality on 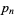. Salvy (1994) deals with more general cases.

B. M. Bredihin proved that

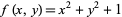(16)

takes prime values for infinitely many integral pairs 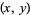 (Honsberger 1976, p. 30). For example, 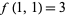, , 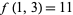, 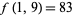and so on. The primes of this form are 3, 11, 19, 41, 53, 59, 73, 83, 101, 107, 131, 137, 149, 163, ... (OEIS A079544; Mitrinović and Sándor 1995, p. 11). The values of  and 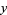 for which  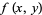is prime are plotted above, showing some interesting patterns.

It is in general not difficult to artificially construct formulas that always generate prime numbers. For example, consider the formula

(17)

where

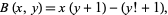(18)

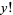 is the factorial, and  and 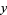 are positive integers (Honsberger 1976, p. 33). This will always have  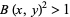and hence yield the value 2 unless  and 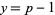, in which case it simplifies to

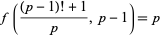(19)

The formula therefore generates odd primes exactly once each (Honsberger 1976, p. 33) at the values for which the Wilson quotient  is an integer, i.e., 1, 1, 5, 103, 329891, 36846277, 1230752346353, ... (OEIS A007619).

The FRACTRAN game (Guy 1983, Conway and Guy 1996, p. 147) provides an unexpected means of generating the prime numbers based on 14 fractions, but it is actually just a concealed version of a sieve.

REFERENCES:

Cipolla, M. ""La determinazione assintotica dell'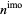 numero primo." Napoli Rend. 3, 132-166, 1902.

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 130 and 147, 1996.

Dudley, U. "History of Formula for Primes." Amer. Math. Monthly 76, 23-28, 1969.

Dusart, P. "The 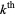 Prime is Greater than  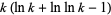for 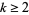." Math. Comput. 68, 411-415, 1999.

Eynden, C. V. "A Proof of Gandhi's Formula for the 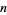th Prime." Amer. Math. Monthly 79, 625, 1972.

Finch, S. R. "Hardy-Littlewood Constants." §2.1 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 84-94, 2003.

Gandhi, J. M. "Formulae for the 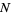th Prime." Proc. Washington State University Conferences on Number Theory. pp. 96-107, 1971.

Gardner, M. "Patterns and Primes." Ch. 9 in The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, pp. 79-90, 1984.

Golomb, S. W. "A Direct Interpretation of Gandhi's Formula." Amer. Math. Monthly 81, 752-754, 1974.

Guy, R. K. "Conway's Prime Producing Machine." Math. Mag. 56, 26-33, 1983.

Guy, R. K. "Prime Numbers," "Formulas for Primes," and "Products Taken over Primes." Ch. A, §A17, and §B48 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 3-43, 36-41, and 102-103, 1994.

Hardy, G. H. and Wright, E. M. "Prime Numbers" and "The Sequence of Primes." §1.2 and 1.4 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 1-4, 5-6, 344-345, and 414, 1979.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.

Honsberger, R. Mathematical Gems II. Washington, DC: Math. Assoc. Amer., 1976.

Mills, W. H. "A Prime-Representing Function." Bull. Amer. Math. Soc. 53, 604, 1947.

Mitrinović, D. S. and Sándor, J. Handbook of Number Theory. Dordrecht, Netherlands: Kluwer, 1995.

Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, 1996.

Ruiz, S. M. "The General Term of the Prime Number Sequence and the Smarandache Prime Function." Smarandache Notions J. 11, 59-61, 2000.

Salvy, B. "Fast Computation of Some Asymptotic Functional Inverses." J. Symb. Comput. 17, 227-236, 1994.

Sloane, N. J. A. Sequences A007619/M4023, A016104, A051021, A051254, A079544, A080339, and A086238 in "The On-Line Encyclopedia of Integer Sequences."

Willans, C. P. "A Formula for the 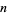th Prime Number." Math. Gaz. 48, 413-415, 1964.

Wright, E. M. "A Prime-Representing Function." Amer. Math. Monthly 58, 616-618, 1951.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم شؤون المعارف يطلق دورة (صفات الشيعة) لعدد من ملاكات العتبة العباسية المقدسة

الهيأة العليا لإحياء التراث تبحث تعزيز التعاون المشترك مع مركز الإمام الباقر (عليه السلام) في إيران

جامعة الكفيل تكرِّم طلبتها المتميزين من ذوي الاحتياجات الخاصة

فريق طبي في مستشفى الكفيل يجري عملية ناجحة لطفل يعاني من تشوّه ولاديّ بالنخاع الشوكي

المزيد

الآخبار الصحية

خصوصا مع تقدم السن.. 6 سلوكيات يومية قد تدمّر صحتك

فاكهة خضراء.. علاج طبيعي فعّال للإمساك واضطرابات الهضم

روسيا تبدأ أولى التجارب السريرية للقاح واعد ضد السرطان

كنز غذائي على طبقك.. ماذا تفعل السبانخ بجسمك؟

المزيد

الآخبار التكنلوجية

رصد نوع نادر من القطط في تايلاند للمرة الأولى منذ عقود

روسيا تخطط لإقامة محطة نووية في القمر خلال العقد المقبل

كيف قاد إيلون ماسك حملة "غروك" لاختراق عرش الذكاء الاصطناعي

ألتمان: الذكاء الاصطناعي سيتجاوز البشر في 2026 !

المزيد