Fermat Quotient

The Fermat quotient for a number 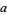 and a prime base  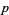is defined as

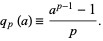(1)

If 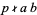, then

			(2)
			(3)

(mod 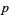), where the modulus is taken as a fractional congruence.

The special case 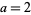 is given by

			(4)
			(5)
			(6)
			(7)
			(8)

all again (mod 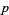) where the modulus is taken as a fractional congruence,  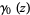is the digamma function, and the last two equations hold for odd primes only.

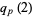 is an integer for  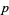a prime, with the values for 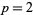, 3, 5, ... being 1, 3, 2, 5, 3, 13, 3, 17, 1, 6, ....

The quantity 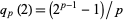 is known to be congruent to zero (mod 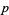) for only two primes: the so-called Wieferich primes 1093 and 3511 (Lehmer 1981, Crandall 1986).

REFERENCES:

Crandall, R. Projects in Scientific Computation. New York: Springer-Verlag, 1986.

Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, p. 105, 2005.

Lehmer, D. H. "On Fermat's Quotient, Base Two." Math. Comput. 36, 289-290, 1981.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 70, 1986.