


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-5-2020
Date: 21-12-2020
Date: 22-10-2020
|
Finch (2001, 2003) defines a 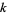 -rough (or
-rough (or 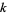 -jagged) number to be positive integer all of whose prime factors are greater than or equal to
-jagged) number to be positive integer all of whose prime factors are greater than or equal to 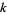 .
.
Greene and Knuth define "unusual numbers" as numbers 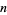 whose greatest prime factor is greater than or equal to
whose greatest prime factor is greater than or equal to 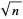 , and these number are dubbed "
, and these number are dubbed "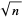 -rough" or "
-rough" or "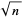 -jagged" by Finch (2001, 2003). The first few unusual numbers are 2, 3, 4, 5, 6, 7, 9, 10, 11, 13, ... (OEIS A063538), which turn out to not be so unusual after all (Greene and Knuth 1990, Finch 2001). The first few "usual" numbers are then 8, 12, 16, 18, 24, 27, 30, ... (OEIS A063539).
-jagged" by Finch (2001, 2003). The first few unusual numbers are 2, 3, 4, 5, 6, 7, 9, 10, 11, 13, ... (OEIS A063538), which turn out to not be so unusual after all (Greene and Knuth 1990, Finch 2001). The first few "usual" numbers are then 8, 12, 16, 18, 24, 27, 30, ... (OEIS A063539).
The probability that the greatest prime factor of a random integer 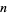 is greater than
is greater than 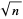 is
is 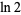 (Schroeppel 1972).
(Schroeppel 1972).
REFERENCES:
Finch, S. "RE: Unusual Numbers." 27 Aug 2001. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0108&L=NMBRTHRY&F=&S=&P=963.
Finch, S. R. "Stieltjes Constants." §2.21 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 166-171, 2003.
Greene, D. H. and Knuth, D. E. Mathematics for the Analysis of Algorithms, 3rd ed. Boston, MA: Birkhäuser, pp. 95-98, 1990.
Schroeppel, R. Item 29 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 13, Feb. 1972. https://www.inwap.com/pdp10/hbaker/hakmem/number.html#item29.
Sloane, N. J. A. Sequences A063538 and A063539 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
الأمين العام للعتبة العسكرية المقدسة يستقبل شيوخ ووجهاء عشيرة البو بدري في مدينة سامراء
|
|
|