Prime Factorization Algorithms

Many algorithms have been devised for determining the prime factors of a given number (a process called prime factorization). They vary quite a bit in sophistication and complexity. It is very difficult to build a general-purpose algorithm for this computationally "hard" problem, so any additional information that is known about the number in question or its factors can often be used to save a large amount of time.

The simplest method of finding factors is so-called "direct search factorization" (a.k.a. trial division). In this method, all possible factors are systematically tested using trial division to see if they actually divide the given number. It is practical only for very small numbers.

The fastest-known fully proven deterministic algorithm is the Pollard-Strassen method (Pomerance 1982; Hardy et al. 1990).

REFERENCES:

Anderson, D. D. (Ed.). Factorization in Integral Domains. New York: Dekker, 1997.

Bressoud, D. M. Factorization and Primality Testing. New York: Springer-Verlag, 1989.

Brillhart, J.; Lehmer, D. H.; Selfridge, J.; Wagstaff, S. S. Jr.; and Tuckerman, B. Factorizations of b-n+/-1, b=2, 3, 5, 6, 7, 10, 11, 12 Up to High Powers, rev. ed. Providence, RI: Amer. Math. Soc., liv-lviii, 1988.

Dickson, L. E. "Methods of Factoring." Ch. 14 in History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, pp. 357-374, 2005.

Hardy, K.; Muskat, J. B.; and Williams, K. S. "A Deterministic Algorithm for Solving 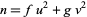 in Coprime Integers  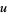and 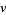." Math. Comput. 55, 327-343, 1990.

Herman, P. "The Factoring Page!" https://www.frenchfries.net/paul/factoring/.

Lenstra, A. K. and Lenstra, H. W. Jr. "Algorithms in Number Theory." In Handbook of Theoretical Computer Science, Volume A: Algorithms and Complexity (Ed. J. van Leeuwen). New York: Elsevier, pp. 673-715, 1990.

Odlyzko, A. M. "The Complexity of Computing Discrete Logarithms and Factoring Integers." §4.5 in Open Problems in Communication and Computation (Ed. T. M. Cover and B. Gopinath). New York: Springer-Verlag, pp. 113-116, 1987.

Odlyzko, A. M. "The Future of Integer Factorization." CryptoBytes: The Technical Newsletter of RSA Laboratories 1, No. 2, 5-12, 1995.

Pomerance, C. "Analysis and Comparison of Some Integer Factorization Algorithms." In Computational Methods in Number Theory, Part 1 (Ed. H. W. Lenstra and R. Tijdeman). Amsterdam, Netherlands: Mathematisch Centrum, pp. 89-139, 1982.

Pomerance, C. "Fast, Rigorous Factorization and Discrete Logarithm Algorithms." In Discrete Algorithms and Complexity (Ed. D. S. Johnson, T. Nishizeki, A. Nozaki, and H. S. Wilf). New York: Academic Press, pp. 119-143, 1987.

Pomerance, C. "A Tale of Two Sieves." Not. Amer. Math. Soc. 43, 1473-1485, 1996.

Riesel, H. "Algebraic Factors." Appendix 6 in Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 304-316, 1994.

Weisstein, E. W. "Books about Prime Numbers." https://www.ericweisstein.com/encyclopedias/books/PrimeNumbers.html.

Williams, H. C. and Shallit, J. O. "Factoring Integers Before Computers." In Mathematics of Computation 1943-1993, Fifty Years of Computational Mathematics (Ed. W. Gautschi). Providence, RI: Amer. Math. Soc., pp. 481-531, 1994.