


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-8-2020
Date: 27-10-2020
Date: 30-9-2020
|
A prime factor is a factor that is prime, i.e., one that cannot itself be factored. In general, a prime factorization takes the form
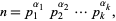 |
(1) |
where 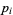 are prime factors and
are prime factors and 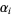 are their orders. Prime factorization can be performed in the Wolfram Language using the command FactorInteger[n], which returns a list of
are their orders. Prime factorization can be performed in the Wolfram Language using the command FactorInteger[n], which returns a list of 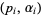 pairs.
pairs.
The following table gives the prime factorization for the positive integers 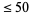 .
.
| 1 | 1 | 11 | 11 | 21 | 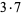 |
31 | 31 | 41 | 41 |
| 2 | 2 | 12 | 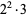 |
22 | 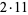 |
32 | 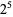 |
42 | 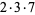 |
| 3 | 3 | 13 | 13 | 23 | 23 | 33 | 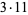 |
43 | 43 |
| 4 | 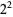 |
14 | 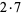 |
24 | 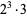 |
34 | 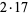 |
44 | 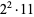 |
| 5 | 5 | 15 | 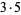 |
25 | 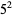 |
35 | 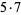 |
45 | 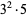 |
| 6 | 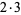 |
16 | 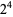 |
26 |  |
36 | 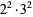 |
46 | 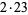 |
| 7 | 7 | 17 | 17 | 27 | 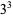 |
37 | 37 | 47 | 47 |
| 8 | 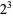 |
18 | 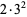 |
28 | 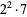 |
38 | 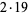 |
48 | 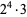 |
| 9 | 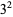 |
19 | 19 | 29 | 29 | 39 | 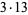 |
49 | 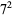 |
| 10 | 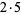 |
20 | 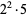 |
30 | 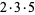 |
40 | 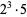 |
50 | 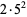 |
The number of not necessarily distinct prime factors of a number  is denoted
is denoted 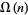 (Hardy and Wright 1979, p. 354) or
(Hardy and Wright 1979, p. 354) or 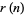 . Conway et al. (2008) coined the term "multiprimality of
. Conway et al. (2008) coined the term "multiprimality of 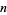 " to describe
" to describe 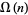 , with semiprimes then being termed biprimes, numbers with three factors terms triprimes, etc. The number of prime factors is given in terms of the prime factorization above by
, with semiprimes then being termed biprimes, numbers with three factors terms triprimes, etc. The number of prime factors is given in terms of the prime factorization above by
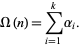 |
(2) |
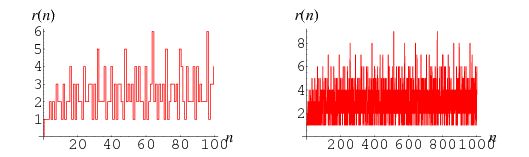
The first few values for 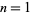 , 2, ... are 0, 1, 1, 2, 1, 2, 1, 3, 2, 2, 1, 3, 1, 2, 2, 4, 1, 3, 1, 3, ... (OEIS A001222).
, 2, ... are 0, 1, 1, 2, 1, 2, 1, 3, 2, 2, 1, 3, 1, 2, 2, 4, 1, 3, 1, 3, ... (OEIS A001222). 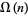 is plotted above up to
is plotted above up to 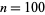 (left) and
(left) and 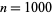 (right). The function
(right). The function 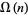 is implemented in the Wolfram Language as PrimeOmega[n],
is implemented in the Wolfram Language as PrimeOmega[n],
The function defined by 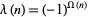 is known as the Liouville function.
is known as the Liouville function.
The number of distinct prime factors of a number 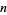 is denoted
is denoted 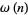 (Hardy and Wright 1979, p. 354), or sometimes
(Hardy and Wright 1979, p. 354), or sometimes 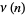 or
or 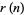 , and is implemented in the Wolfram Language as PrimeNu[n].
, and is implemented in the Wolfram Language as PrimeNu[n].
For example, 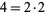 has a single distinct prime factor, so
has a single distinct prime factor, so 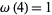 , but two total prime factors, so
, but two total prime factors, so 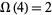 .
.
An asymptotic series for 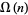 is given by
is given by
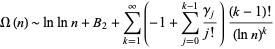 |
(3) |
(Diaconis 1976, Knuth 2000, Diaconis 2002, Finch 2003, Knuth 2003), where 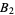 is a constant related to the Mertens constant and
is a constant related to the Mertens constant and 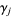 are Stieltjes constants. Furthermore, the variance is given by
are Stieltjes constants. Furthermore, the variance is given by
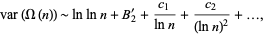 |
(4) |
where
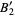 |
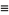 |
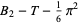 |
(5) |
 |
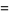 |
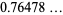 |
(6) |
(OEIS A091589), and
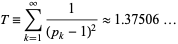 |
(7) |
(OEIS A086242; Finch 2003) is a convergent prime sum. The coefficients 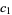 and
and 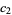 are given by the sums
are given by the sums
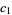 |
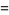 |
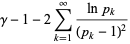 |
(8) |
 |
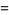 |
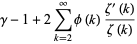 |
(9) |
 |
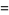 |
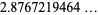 |
(10) |
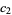 |
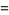 |
![-gamma_1-(gamma-1)[gamma-2sum_(k=1)^(infty)(lnp_k)/((p_k-1)^2)]-2sum_(k=1)^(infty)(p_k(lnp_k)^2)/((p_k-1)^3)](https://mathworld.wolfram.com/images/equations/PrimeFactor/Inline79.gif) |
(11) |
 |
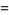 |
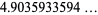 |
(12) |
(Diaconis 1976, Knuth 2000, Diaconis 2002, Finch 2003, Knuth 2003), where
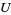 |
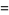 |
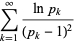 |
(13) |
 |
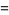 |
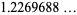 |
(14) |
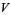 |
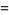 |
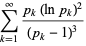 |
(15) |
 |
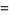 |
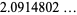 |
(16) |
(Finch 2003).
Similarly, if 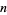 is chosen at random between 1 and
is chosen at random between 1 and  , then the probability that
, then the probability that
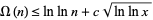 |
(17) |
approaches
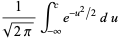 |
(18) |
as 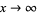 (Knuth 1998, p. 384). In addition, the average value
(Knuth 1998, p. 384). In addition, the average value 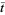 of
of 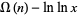 for
for 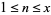 approaches
approaches 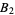 (Erdős and Kac 1940; Hardy and Wright 1979; Knuth 1998, p. 384)
(Erdős and Kac 1940; Hardy and Wright 1979; Knuth 1998, p. 384)

The average order of 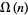 is
is
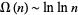 |
(19) |
(Hardy 1999, p. 51). More precisely,
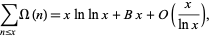 |
(20) |
for appropriate constants 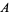 and
and 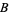 (Hardy and Ramanujan 1917; Hardy and Wright 1979, p. 355; Hardy 1999, p. 57), where
(Hardy and Ramanujan 1917; Hardy and Wright 1979, p. 355; Hardy 1999, p. 57), where 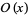 is asymptotic notation.
is asymptotic notation.
REFERENCES:
Conway, J. H.; Dietrich, H.; O'Brien, E. A. "Counting Groups: Gnus, Moas, and Other Exotica." Math. Intell. 30, 6-18, 2008.
Diaconis, P. "Asymptotic Expansions for the Mean and Variance of the Number of Prime Factors of a Number 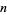 ." Dept. Statistics Tech. Report 96, Stanford, CA: Stanford University, 1976.
." Dept. Statistics Tech. Report 96, Stanford, CA: Stanford University, 1976.
Diaconis, P. "G. H. Hardy and Probability???" Bull. London Math. Soc. 34, 385-402, 2002.
Erdős, P. and Kac, M. "The Gaussian Law of Errors in the Theory of Additive Number Theoretic Functions." Amer. J. Math. 26, 738-742, 1940.
Finch, S. "Two Asymptotic Series." December 10, 2003. https://algo.inria.fr/bsolve/.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Hardy, G. H. and Ramanujan, S. Quart. J. Math. 48, 76-92, 1917.
Hardy, G. H. and Wright, E. M. §22.11 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Knuth, D. E. The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 3rd ed. Reading, MA: Addison-Wesley, p. 384, 1998.
Knuth, D. E. Selected Papers on Analysis of Algorithms. Stanford, CA: CSLI Publications, pp. 338-339, 2000.
Ramanujan, S. Collected Papers of Srinivasa Ramanujan (Ed. G. H. Hardy, P. V. S. Aiyar, and B. M. Wilson). Providence, RI: Amer. Math. Soc., p. 327, 2000.
Sloane, N. J. A. Sequences A001222/M0094, A001221/M0056, A030059, A083342, A086242, and A091589 in "The On-Line Encyclopedia of Integer Sequences."
Turán, P. "On a Theorem of Hardy and Ramanujan." J. London Math. Soc. 9, 274-276, 1934.
Turán, P. "Über einige Verallgemeinerungen eines Satzes von Hardy und Ramanujan." J. London Math. Soc. 11, 125-133, 1936.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|