Pratt Certificate

The Pratt certificate is a primality certificate based on Fermat's little theorem converse. Prior to the work of Pratt (1975), the Lucas-Lehmer test had been regarded purely as a heuristic that worked a lot of the time (Knuth 1969). Pratt (1975) showed that Lehmer's primality heuristic could be made a nondeterministic procedure by applying it recursively to the factors of 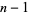. As a consequence of this result, Pratt (1975) became the first to demonstrate that the resulting tree implies that prime factorization lies in the complexity class NP.

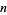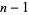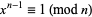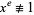To generate a Pratt certificate, assume that  is a positive integer and  is the set of prime factors of . Suppose there exists an integer  (called a "witness") such that  but  (mod 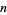) whenever  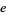is one of 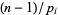. Then Fermat's little theorem converse states that  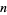is prime (Wagon 1991, pp. 278-279).

By applying Fermat's little theorem converse to 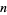 and recursively to each purported factor of 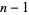, a certificate for a given prime number can be generated. Stated another way, the Pratt certificate gives a proof that a number  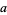is a primitive root of the multiplicative group (mod 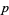) which, along with the fact that  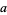has order 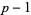, proves that  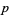is a prime.

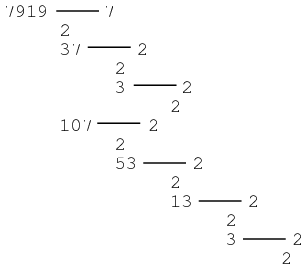
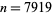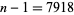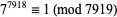The figure above gives a certificate for the primality of . The numbers to the right of the dashes are witnesses to the numbers to left. The set  for  is given by . Since  but 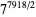, , 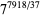 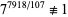(mod 7919), 7 is a witness for 7919. The prime divisors of  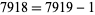are 2, 37, and 107. 2 is a so-called "self-witness" (i.e., it is recognized as a prime without further ado), and the remainder of the witnesses are shown as a nested tree. Together, they certify that 7919 is indeed prime. Because it requires the factorization of 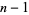, the method of Pratt certificates is best applied to small numbers (or those numbers  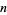known to have easily factorable ).

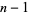A Pratt certificate is quicker to generate for small numbers than are other types of primality certificates. The Wolfram Language function ProvablePrimeQ[n] in the Wolfram Language package PrimalityProving` therefore generates an Atkin-Goldwasser-Kilian-Morain certificate only for numbers above a certain limit (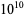 by default), and a Pratt certificate for smaller numbers.

REFERENCES:

Knuth, D. E. §4.5.4 in The Art of Computer Programming, Vol. 2: Seminumerical Algorithms. Reading, MA: Addison-Wesley, 1969.

Pratt, V. "Every Prime Has a Succinct Certificate." SIAM J. Comput. 4, 214-220, 1975.

Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 278-285, 1991.

Wilf, H. §4.10 in Algorithms and Complexity. Englewood Cliffs, NJ: Prentice-Hall, 1986.