Cluster Prime

An odd prime 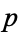 is called a cluster prime if every even positive integer less than  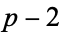can be written as a difference of two primes 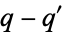, where 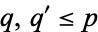. The first 23 odd primes 3, 5, 7, ..., 89 are all cluster primes. The first few odd primes that are not cluster primes are 97, 127, 149, 191, 211, ... (OEIS A038133).

The numbers of cluster primes less than 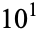, , 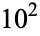... are 23, 99, 420, 1807, ... (OEIS A039506), and the corresponding numbers of noncluster primes are 0, 1, 68, 808, 7784, ... (OEIS A039507). It is not known if there are infinitely many cluster primes, but Blecksmith et al. (1999) show that for every positive integer 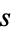, there is a bound  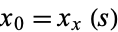such that if 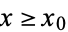, then

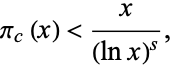where 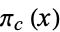 is the number of cluster primes not exceeding 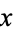. Blecksmith et al. (1999) also show that the sum of the reciprocals of the cluster primes is finite.

REFERENCES:

Blecksmith, R.; Erdős, P.; and Selfridge, J. L. "Cluster Primes." Amer. Math. Monthly 106, 43-48, 1999.

Elsholtz, C. "On Cluster Primes." Acta Arith. 109, 281-284, 2003.

Sloane, N. J. A. Sequences A038133, A039506, and A039507 in "The On-Line Encyclopedia of Integer Sequences."