


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-1-2020
Date: 29-3-2020
Date: 20-7-2020
|
Cubic lattice sums include the following:
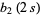 |
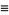 |
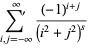 |
(1) |
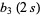 |
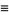 |
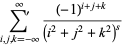 |
(2) |
 |
 |
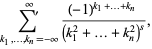 |
(3) |
where the prime indicates that the origin 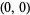 ,
, 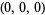 , etc. is excluded from the sum (Borwein and Borwein 1986, p. 288).
, etc. is excluded from the sum (Borwein and Borwein 1986, p. 288).
These have closed forms for even 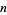 ,
,
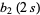 |
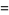 |
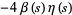 |
(4) |
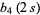 |
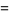 |
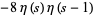 |
(5) |
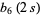 |
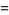 |
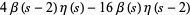 |
(6) |
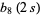 |
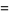 |
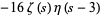 |
(7) |
for ![R[s]>1](https://mathworld.wolfram.com/images/equations/LatticeSum/Inline25.gif) , where
, where 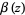 is the Dirichlet beta function,
is the Dirichlet beta function, 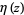 is the Dirichlet eta function, and
is the Dirichlet eta function, and 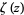 is the Riemann zeta function (Zucker 1974, Borwein and Borwein 1987, pp. 288-301). The lattice sums evaluated at
is the Riemann zeta function (Zucker 1974, Borwein and Borwein 1987, pp. 288-301). The lattice sums evaluated at 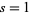 are called the Madelung constants. An additional form for
are called the Madelung constants. An additional form for 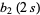 is given by
is given by
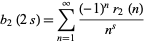 |
(8) |
for ![R[s]>1/3](https://mathworld.wolfram.com/images/equations/LatticeSum/Inline31.gif) , where
, where 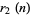 is the sum of squares function, i.e., the number of representations of
is the sum of squares function, i.e., the number of representations of 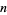 by two squares (Borwein and Borwein 1986, p. 291). Borwein and Borwein (1986) prove that
by two squares (Borwein and Borwein 1986, p. 291). Borwein and Borwein (1986) prove that 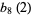 converges (the closed form for
converges (the closed form for 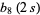 above does not apply for
above does not apply for 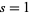 ), but its value has not been computed. A number of other related double series can be evaluated analytically.
), but its value has not been computed. A number of other related double series can be evaluated analytically.
For hexagonal sums, Borwein and Borwein (1987, p. 292) give
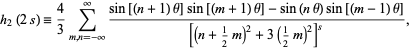 |
(9) |
where 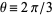 . This Madelung constant is expressible in closed form for
. This Madelung constant is expressible in closed form for 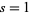 as
as
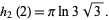 |
(10) |
Other interesting analytic lattice sums are given by
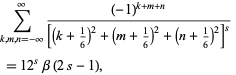 |
(11) |
giving the special case
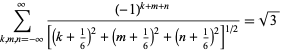 |
(12) |
(Borwein and Borwein 1986, p. 303), and
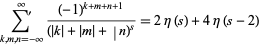 |
(13) |
(Borwein and Borwein 1986, p. 305).
REFERENCES:
Borwein, D. and Borwein, J. M. "A Note on Alternating Series in Several Dimensions." Amer. Math. Monthly 93, 531-539, 1986.
Borwein, D. and Borwein, J. M. "On Some Trigonometric and Exponential Lattice Sums." J. Math. Anal. 188, 209-218, 1994.
Borwein, D.; Borwein, J. M.; and Shail, R. "Analysis of Certain Lattice Sums." J. Math. Anal. 143, 126-137, 1989.
Borwein, D.; Borwein, J. M.; and Taylor, K. F. "Convergence of Lattice Sums and Madelung's Constant." J. Math. Phys. 26, 2999-3009, 1985.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.
Finch, S. R. "Madelung's Constant." §1.10 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 76-81, 2003.
Glasser, M. L. and Zucker, I. J. "Lattice Sums." In Perspectives in Theoretical Chemistry: Advances and Perspectives, Vol. 5 (Ed. H. Eyring).
Zucker, I. J. "Exact Results for Some Lattice Sums in 2, 4, 6 and 8 Dimensions." J. Phys. A: Nucl. Gen. 7, 1568-1575, 1974.



|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
الزائرون يحيون ليلة الجمعة الأخيرة من شهر ربيع الآخر عند مرقد أبي الفضل العبّاس (عليه السلام)
|
|
|