
Small Numbers (2)
 المؤلف:
Daiev, V.
المؤلف:
Daiev, V.
 المصدر:
"Problem 636: Greatest Divisors of Even Integers." Math. Mag. 40
المصدر:
"Problem 636: Greatest Divisors of Even Integers." Math. Mag. 40
 الجزء والصفحة:
...
الجزء والصفحة:
...
 11-8-2020
11-8-2020
 973
973
Small Numbers (2)
The number two is the second positive integer and the first prime number. It is even, and is the only even prime (the primes other than 2 are called the odd primes). The number 2 is also equal to its factorial since 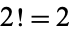 . A quantity taken to the power 2 is said to be squared. The number of times
. A quantity taken to the power 2 is said to be squared. The number of times 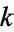 a given binary number
a given binary number 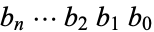 is divisible by 2 is given by the position of the first
is divisible by 2 is given by the position of the first 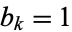 , counting from the right. For example,
, counting from the right. For example, 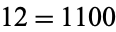 is divisible by 2 twice, and
is divisible by 2 twice, and 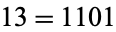 is divisible by 2 zero times.
is divisible by 2 zero times.
The only known solutions to the congruence
are summarized in the following table (OEIS A050259). M. Alekseyev explored all solutions below 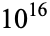 on Jan. 27 2007, finding no other solutions in this range.
on Jan. 27 2007, finding no other solutions in this range.
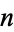 |
reference |
| 4700063497 |
Guy (1994) |
| 3468371109448915 |
M. Alekseyev (pers. comm., Nov. 13, 2006) |
| 8365386194032363 |
Crump (pers. comm., 2000) |
| 10991007971508067 |
Crump (2007) |
| 63130707451134435989380140059866138830623361447484274774099906755 |
Montgomery (1999) |
In general, the least 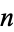 satisfying
satisfying
for 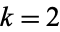 , 3, ... are
, 3, ... are 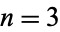 , 4700063497, 6, 19147, 10669, 25, 9, 2228071, ... (OEIS A036236).
, 4700063497, 6, 19147, 10669, 25, 9, 2228071, ... (OEIS A036236).
The chorus of the song "Power of Two" by the Indigo Girls (Swamp Ophelia, 1994), includes the lines "Adding up the total of a love that's true; Multiply life by the power of two."
REFERENCES:
Crump, J. "2n mod n = c." http://www.immortaltheory.com/NumberTheory/2nmodn.htm.
Crump, J. "2^n = 3 (mod n): New Solution: 10991007971508067." 22 Jan 2007. http://listserv.nodak.edu/cgi-bin/wa.exe?A2=ind0701&L=nmbrthry&T=0&P=3310.
Daiev, V. "Problem 636: Greatest Divisors of Even Integers." Math. Mag. 40, 164-165, 1967.
Guy, R. K. "Residues of Powers of Two." §F10 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 250, 1994.
Montgomery, P.-L. "New solution to 2^n == 3 (mod n)." 24 Jun 1999. http://listserv.nodak.edu/scripts/wa.exe?A2=ind9906&L=NMBRTHRY&F=&S=&P=1753.
Sloane, N. J. A. Sequences A036236 and A050259 in "The On-Line Encyclopedia of Integer Sequences."
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 41-44, 1986.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


