The energy integral
المؤلف:
A. Roy, D. Clarke
المصدر:
Astronomy - Principles and Practice 4th ed
الجزء والصفحة:
p 176
11-8-2020
2175
The energy integral
If we multiply equation (1)
(1)
by dx/dt and 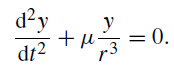(2)
(2)
by dy/dt and add, we obtain the relation
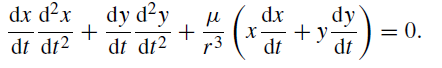(3)
Now
Also, r 2 = x2 + y2 so that
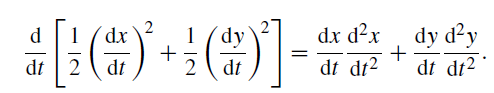
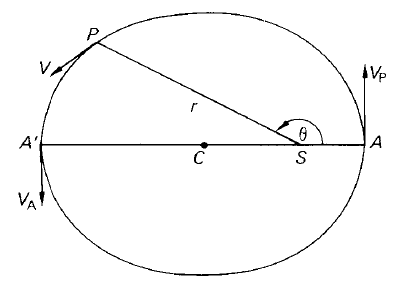
Figure 1. The velocity of a planet in an elliptical orbit showing that at perihelion A and aphelion A' the velocity vector is perpendicular to the radius vector.
giving
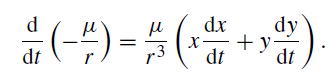
Hence, equation (3) may be written as a perfect differential, namely
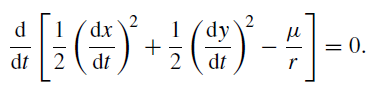
Integrating, we obtain
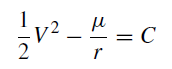(4)
where C is the so-called energy constant and V is the velocity of one mass with respect to the other since
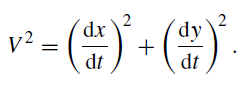
The first term, 1/2 V 2, is the kinetic energy, energy the planet in its orbit about the Sun possesses by virtue of its speed. The second term, −μ/r, is the potential energy, energy the planet possesses by
virtue of its distance from the Sun.
What equation (4) states is that the sum of these two energies is a constant, a reasonable statement since the two-body is an isolated system, no energy being injected into the system or being removed from it. In an elliptic orbit, however, the distance r is changing. Equation (4) shows that there is a continual trade-off between the two energies: when one is increasing, the other is decreasing. If we wish to obtain an expression giving the velocity V of the planet, we must interpret the constant C. This is done in the following section.
الاكثر قراءة في مواضيع عامة في علم الفلك
اخر الاخبار
اخبار العتبة العباسية المقدسة
