Geocentric motion of a planet
 

Once the sidereal period T of a planet is found, also the mean heliocentric distance a, the velocity V
of the planet in its orbit (assumed circular) can be calculated. Thus,

For two planets, therefore, the ratio of their orbital velocities is given by
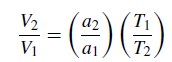(1)
where the subscripts 1 and 2 refer to the inner and outer planet respectively. Putting in values, it is found that the velocity of the inner planet is greater than that of the outer. As we shall see later, Kepler found that for any planet,
a³ ∝ T ²
or
a³ = kT² (2)
where k is a constant.
Then by equation (2),

According to Kepler, therefore, we may write for the two planets,

Substituting for T1 and T2 in equation (12.3), we obtain,

(3)

In figure 1, the orbits of the Earth and a planet are shown, the radii of the orbits (assumed
circular and coplanar) being a and b units respectively. Since the planet is a superior one, b is greater
than a.
At opposition, the positions of the planet and Earth are P₁ and E₁ and their velocity vectors are shown as V_P and V_⊕ respectively, tangential to their orbits.
Now by equation (3), V_P < V_⊕ and so the angular velocity of the planet as observed from the Earth is

and is in a direction opposite to the orbital movement. It is, therefore, retrograde at opposition.

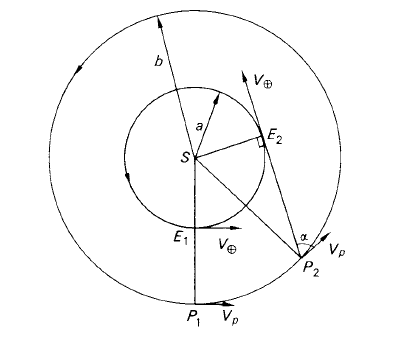
Figure 1. The velocities of the Earth and a superior planet produce retrograde motion of the planet (P₁) at opposition and direct motion of the planet (P₂) at quadrature.
At the following quadrature, the positions of planet and Earth are P₂ and E₂, where ∠SE₂P₂ = 90^◦. The Earth’s orbital velocity V_⊕ is now along the line P₂E₂ but the planet’s velocity VP has a component V_P sin α, perpendicular to E₂P₂. The other component VP cos α lies along the line P₂E₂ and, like the Earth’s velocity V_⊕, does not contribute to the observed angular velocity of the planet. This geocentric angular velocity at quadrature is, therefore,

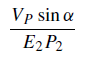
and is seen to be in the same direction as the orbital movement. It is thus direct at quadrature.

اخر الاخبار

اخبار العتبة العباسية المقدسة

جولة تفقدية لمتابعة خطة تنظيم مداخل المعزّين المشاركين في عزاء ركضة طويريج

لتعزيز التعاون الأكاديمي والبحثي.. جامعة الكفيل توقع اتفاقيتي توأمة مع جامعتين عراقيتين

المجمَع العلميّ يواصل إقامة مجلسه العزائي بذكرى شهادة الإمام الحسين (عليه السلام) في النجف الأشرف

قسم حفظ النظام يواصل تنفيذ خطته لتنظيم سير المواكب والزائرين في شهر المحرم

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد

مواضيع ذات صلة

اختبار الانفجار الهائل

الكوسمولوجيا وأشكال كالابي - ياو

التخمينات الكوسمولوجيا والنظرية النهائية

النموذج القياسي للكوسمولوجيا، أو علم الكون

تأملات في علم الكون

المذنبات

الصعود إلى الفضاء

اختلاف الليل والنهار

تصنيع الصاروخ و اطلاقة

الكويكبات والمذنبات

صورة الحجر الأزتكي (فهم وإدراك الحضارة الآزيتية )

الهالات المجرية