The ecliptic system of coordinates
 

This system is specially convenient in studying themovements of the planets and in describing the Solar System. The two quantities specifying the position of an object on the celestial sphere in this system are ecliptic longitude and ecliptic latitude. In figure 1 a great circle arc through the pole of the ecliptic K and the celestial object X meets the ecliptic in the point D. Then the ecliptic longitude, λ, is the angle between and D, measured from 0◦ to 360◦ along the ecliptic in the eastwards direction, that is in the direction in which right ascension increases. The ecliptic latitude, β, is measured from D to X along the great circle arc DX, being measured from 0◦ to 90◦ north or south of the ecliptic. It should be noted that the north pole of the ecliptic, K, lies in the hemisphere containing the north celestial pole. It should also be noted that ecliptic latitude and longitude are often referred to as celestial latitude and longitude.

Figure 1. Ecliptic coordinates.

The point of intersection Aries () of the celestial equator and the ecliptic is often referred to as the ascending node, since an object travelling in the plane of the ecliptic with the direction of increasing right ascension (eastwards) passes through Aries from southern to northern declinations.
By similar reasoning, Libra () is called the descending node. The origins most often used with this system of coordinates are the Earth’s centre and the Sun’s centre since most of the planets move in planes inclined only a few degrees to the ecliptic.
It is often required to convert from the ecliptic system to equatorial coordinates, i.e. the system of right ascension and declination or vice versa. This may be achieved by considering the spherical triangle K PX in figure 8.19, where ∠K PX = 90^◦ + α, α being the right ascension of X, or B, while BX is the object’s declination, δ. Let us suppose α, δ are known, also the obliquity of the ecliptic, and it is required to calculate, λ, β. Then, using the cosine formula,
cos(90 − β) = cos ε cos(90 − δ) + sin ε sin(90 − δ) cos(90 + α)
or
sin β = cos ε sin δ − sin ε cos δ sin α. (1)
Applying the cosine formula once more, we have
cos(90 − δ) = cos ε cos(90 − β) + sin ε sin(90 − β) cos(90 − λ)

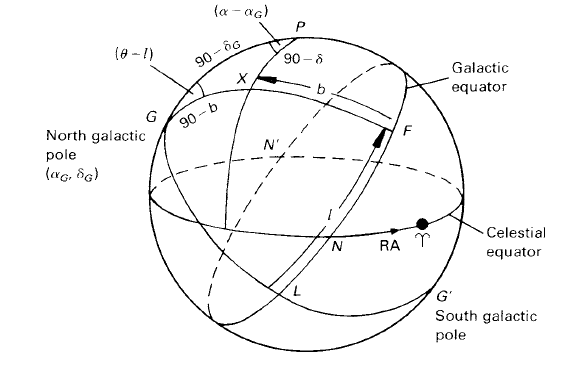
Figure 2. Galactic coordinates.
 

that is
sin δ = cos ε sin β + sin ε cos β sin λ
or
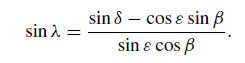.............(1)
Values for λ may be obtained directly from α, δ by substituting for β in equation (1), so providing a formula for the calculation of λ given by
......(2)
The quadrant associated with λ can be elucidated by noting the signs of the numerator and denominator in either of the equations (1) or (2).
Alternatively, these identities could have been derived using the the four-parts formula. The solution of the problem in reverse (given λ, β, ε; find α, δ) is left to the reader.