Informally, an elliptic curve is a type of cubic curve whose solutions are confined to a region of space that is topologically equivalent to a torus. The Weierstrass elliptic function 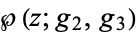 describes how to get from this torus to the algebraic form of an elliptic curve.

Formally, an elliptic curve over a field 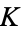 is a nonsingular cubic curve in two variables, 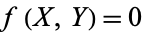, with a -rational point (which may be a point at infinity). The field 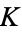 is usually taken to be the complex numbers 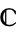, reals 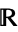, rationals 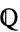, algebraic extensions of 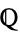, p-adic numbers 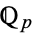, or a finite field.

By an appropriate change of variables, a general elliptic curve over a field with field characteristic 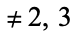, a general cubic curve

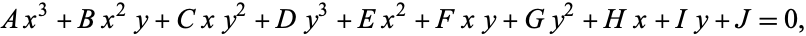(1)

where 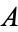, , 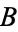..., are elements of 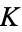, can be written in the form

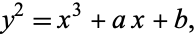(2)

where the right side of (2) has no repeated factors. Any elliptic curve not of characteristic 2 or 3 can also be written in Legendre normal form

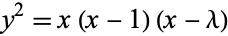(3)

(Hartshorne 1999).

Elliptic curves are illustrated above for various values of 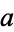 and .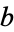

If 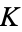 has field characteristic three, then the best that can be done is to transform the curve into

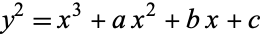(4)

(the 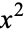 term cannot be eliminated). If  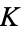has field characteristic two, then the situation is even worse. A general form into which an elliptic curve over any  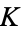can be transformed is called the Weierstrass form, and is given by

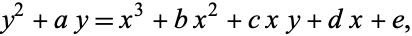(5)

where 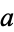, , 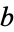, , 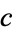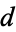and 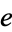 are elements of 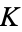. Luckily, 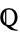, , 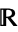and 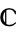 all have field characteristic zero.

An elliptic curve of the form 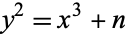 for 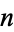 an integer is known as a Mordell curve.

Whereas conic sections can be parameterized by the rational functions, elliptic curves cannot. The simplest parameterization functions are elliptic functions. Abelian varieties can be viewed as generalizations of elliptic curves.

If the underlying field of an elliptic curve is algebraically closed, then a straight line cuts an elliptic curve at three points (counting multiple roots at points of tangency). If two are known, it is possible to compute the third. If two of the intersection points are 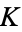-rational, then so is the third. Mazur and Tate (1973/74) proved that there is no elliptic curve over  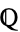having a rational point of order 13.

Let 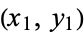 and 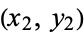 be two points on an elliptic curve  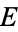with elliptic discriminant

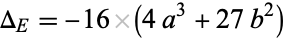(6)

satisfying

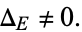(7)

A related quantity known as the j-invariant of 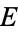 is defined as

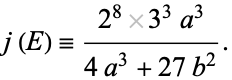(8)

Now define

{(y_1-y_2)/(x_1-x_2) for x_1!=x_2; (3x_1^2+a)/(2y_1) for x_1=x_2. " src="https://mathworld.wolfram.com/images/equations/EllipticCurve/NumberedEquation9.gif" style="height:86px; width:168px" />

(9)

Then the coordinates of the third point are

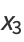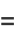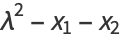			(10)
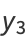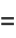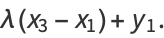			(11)

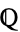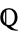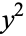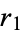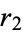For elliptic curves over , Mordell proved that there are a finite number of integral solutions. The Mordell-Weil theorem says that the group of rational points of an elliptic curve over  is finitely generated. Let the roots of  be , , and 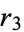. The discriminant is then

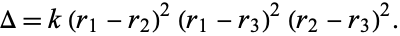(12)

The amazing Taniyama-Shimura conjecture states that all rational elliptic curves are also modular. This fact is far from obvious, and despite the fact that the conjecture was proposed in 1955, it was not even partially proved until 1995. Even so, Wiles' proof for the semistable case surprised most mathematicians, who had believed the conjecture unassailable. As a side benefit, Wiles' proof of the Taniyama-Shimura conjecture also laid to rest the famous and thorny problem which had baffled mathematicians for hundreds of years, Fermat's last theorem.

Curves with small j-conductors are listed in Swinnerton-Dyer (1975) and Cremona (1997). Methods for computing integral points (points with integral coordinates) are given in Gebel et al. and Stroeker and Tzanakis (1994). The Schoof-Elkies-Atkin algorithm can be used to determine the order of an elliptic curve 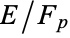 over the finite field .

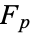REFERENCES:

Atkin, A. O. L. and Morain, F. "Elliptic Curves and Primality Proving." Math. Comput. 61, 29-68, 1993.

Cassels, J. W. S. Lectures on Elliptic Curves. New York: Cambridge University Press, 1991.

Cremona, J. E. Algorithms for Modular Elliptic Curves, 2nd ed. Cambridge, England: Cambridge University Press, 1997.

Cremona, J. E. "Elliptic Curve Data." https://modular.fas.harvard.edu/cremona/INDEX.html.

Du Val, P. Elliptic Functions and Elliptic Curves. Cambridge, England: Cambridge University Press, 1973.

Fermigier, S. "Collection of Links on Research Articles on Elliptic Curves and Related Topics." https://www.fermigier.com/fermigier/elliptic.html.en.

Gebel, J.; Pethő, A.; and Zimmer, H. G. "Computing Integral Points on Elliptic Curves." Acta Arith. 68, 171-192, 1994.

Hartshorne, R. Algebraic Geometry. New York: Springer-Verlag, 1999.

Ireland, K. and Rosen, M. "Elliptic Curves." Ch. 18 in A Classical Introduction to Modern Number Theory, 2nd ed. New York: Springer-Verlag, pp. 297-318, 1990.

Joye, M. "Some Interesting References on Elliptic Curves." https://www.geocities.com/MarcJoye/biblio_ell.html.

Katz, N. M. and Mazur, B. Arithmetic Moduli of Elliptic Curves. Princeton, NJ: Princeton University Press, 1985.

Knapp, A. W. Elliptic Curves. Princeton, NJ: Princeton University Press, 1992.

Koblitz, N. Introduction to Elliptic Curves and Modular Forms. New York: Springer-Verlag, 1993.

Lang, S. Elliptic Curves: Diophantine Analysis. Berlin: Springer-Verlag, 1978.

Mazur, B. and Tate, J. "Points of Order 13 on Elliptic Curves." Invent. Math. 22, 41-49, 1973/74.

McKean, H. and Moll, V. Elliptic Curves: Function Theory, Geometry, Arithmetic. Cambridge, England: Cambridge University Press, 1999.

Riesel, H. "Elliptic Curves." Appendix 7 in Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 317-326, 1994.

Silverman, J. H. The Arithmetic of Elliptic Curves. New York: Springer-Verlag, 1986.

Silverman, J. H. The Arithmetic of Elliptic Curves II. New York: Springer-Verlag, 1994.

Silverman, J. H. and Tate, J. T. Rational Points on Elliptic Curves. New York: Springer-Verlag, 1992.

Stillwell, J. "Elliptic Curves." Amer. Math. Monthly 102, 831-837, 1995.

Stroeker, R. J. and Tzanakis, N. "Solving Elliptic Diophantine Equations by Estimating Linear Forms in Elliptic Logarithms." Acta Arith. 67, 177-196, 1994.

Swinnerton-Dyer, H. P. F. "Correction to: 'On 1-adic Representations and Congruences for Coefficients of Modular Forms.' " In Modular Functions of One Variable, Vol. 4, Proc. Internat. Summer School for Theoret. Phys., Univ. Antwerp, Antwerp, RUCA, July-Aug. 1972. Berlin: Springer-Verlag, 1975.

Weisstein, E. W. "Books about Elliptic Curves." https://www.ericweisstein.com/encyclopedias/books/EllipticCurves.html.

اخر الاخبار

اخبار العتبة العباسية المقدسة

ما الخدمات التي قدّمها موكب أشبال الطفّ لزائري عاشوراء؟

العتبة العباسية المقدسة تنظّم مسيرات عزائية لإحياء ذكرى عاشوراء في نينوى

قسم الشؤون الفكرية يحيي ذكرى استشهاد الإمام الحسين (عليه السلام) في القارة الإفريقية

قسمُ التربية والتعليم يقيم مجلسه العزائي السنوي بذكرى عاشوراء

المزيد

الآخبار الصحية

تناول الجبن.. مفيد للجسم أم خطر يهدد صحتك؟

طبيبة أسنان تحذر.. لا تتجاهل هذه العلامة بعد التنظيف

يجب أن تأكل المزيد من الشمام هذا الصيف.. إليك السبب ؟

تأثير صحي كبير.. كم بيضة يجب أن تتناول يوميا؟

المزيد

الآخبار التكنلوجية

أداء خلايا البيروفسكايت الشمسية تحت الماء قد يزيد كفاءة تحويل الكهرباء

مسافة الأمان: أساس القيادة الآمنة وتجنب الحوادث

هل القيادة السريعة تعني استهلاك اكثر للوقود؟

لماذا يعتبر كوكب المريخ غير صالح للحياة؟

المزيد