Infinitary Divisor
المؤلف:
Guy, R. K.
المصدر:
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag
الجزء والصفحة:
...
26-6-2020
1397
Infinitary Divisor
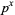is an infinitary divisor of 
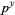(with 
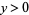) if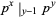 
, where 
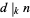denotes a k-ary Divisor (Guy 1994, p. 54). Infinitary divisors therefore generalize the concept of the k-ary divisor.
Infinitary divisors can also be defined as follows. Compute the prime factorization for each divisor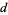 
of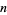 
,
Now make a table of the binary representations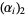 
of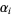 
for each prime factor 
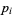. The infinitary divisors are then those factors 
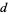that have zeros in the binary representation of all 
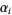s where 
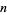itself does. This is illustrated in the following table for the number 
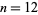, which has divisors 1, 2, 3, 4, 6, and 12 and prime factors 2 and 3.
 |
 |
 |
 |
 |
 |
 |
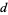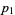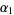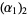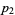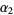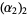| 1 |
2 |
0 |
000 |
3 |
0 |
000 |
| 2 |
2 |
1 |
001 |
3 |
0 |
000 |
| 3 |
2 |
0 |
000 |
3 |
1 |
001 |
| 4 |
2 |
2 |
010 |
3 |
0 |
000 |
| 6 |
2 |
1 |
001 |
3 |
1 |
001 |
| 12 |
2 |
2 |
010 |
3 |
1 |
001 |
As can be seen from the table, the divisors 1, 3, 4, and 12 have zeros in the binary expansions of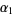 
(the exponents of 2) in the positions that 12 itself does. Similarly, all divisors have zeros in the leftmost two positions in the binary expansions of 
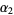(the exponents of 3), as does 12 itself. The intersection of the divisors matching zero in the binary representations in each of the exponents is therefore 1, 3, 4, 12, and these are the infinitary divisors of 12.
The following table lists the infinitary divisors for small integers (OEIS A077609).
 |
 |
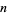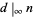| 1 |
1 |
| 2 |
1, 2 |
| 3 |
1, 3 |
| 4 |
1, 4 |
| 5 |
1, 5 |
| 6 |
1, 2, 3, 6 |
| 7 |
1, 7 |
| 8 |
1, 2, 4, 8 |
| 9 |
1, 9 |
| 10 |
1, 2, 5, 10 |
| 11 |
1, 11 |
| 12 |
1, 3, 4, 12 |
| 13 |
1, 13 |
| 14 |
1, 2, 7, 14 |
| 15 |
1, 3, 5, 15 |
The numbers of infinitary divisors of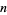 
for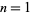 
, 2, ... are 1, 2, 2, 2, 2, 4, 2, 4, 2, 4, ... (OEIS A037445).
REFERENCES:
Abbott, P. "In and Out: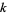 
-ary Divisors." Mathematica J. 9, 702-706, 2005.
Cohen, G. L. "On an Integer's Infinitary Divisors." Math. Comput. 54, 395-411, 1990.
Cohen, G. and Hagis, P. "Arithmetic Functions Associated with the Infinitary Divisors of an Integer." Internat. J. Math. Math. Sci. 16, 373-383, 1993.
Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 54, 1994.
Sloane, N. J. A. Sequences A037445 and A077609 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
