


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-12-2019
Date: 12-11-2019
Date: 21-12-2019
|
A Thue equation is a Diophantine equation of the form
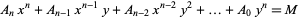 |
in terms of an irreducible polynomial of degree 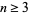 having coefficients
having coefficients 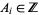 for which solutions in integers
for which solutions in integers  and
and 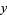 are sought for each given constant
are sought for each given constant 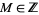 with
with 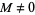 .
.
Thue (1909) proved that such an equation has only finitely many solutions, but it was not until much later that Tzanakis and de Weger (1989) gave a practical algorithm for finding bounds on 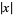 and
and 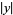 . Although these bounds can be astronomically large in some cases, they are typically small enough to allow an exhaustive search for all solutions.
. Although these bounds can be astronomically large in some cases, they are typically small enough to allow an exhaustive search for all solutions.
REFERENCES:
Thue, A. "Über Annäherungswerte algebraischer Zahlen." J. reine angew. Math. 135, 284-305, 1909.
Tzanakis, N. and de Weger, B. M. M. "On the Practical Solution of the Thue Equation." J. Number Th. 31, 99-132, 1989.



|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
المجمع العلميّ يُواصل عقد جلسات تعليميّة في فنون الإقراء لطلبة العلوم الدينيّة في النجف الأشرف
|
|
|