


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-1-2021
Date: 31-10-2019
Date: 10-4-2020
|
An idoneal number, also called a suitable number or convenient number, is a positive integer 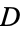 for which the fact that a number is a monomorph (i.e., is expressible in only one way as
for which the fact that a number is a monomorph (i.e., is expressible in only one way as 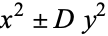 where
where 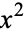 is relatively prime to
is relatively prime to 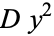 ) guarantees it to be a prime, prime power, or twice one of these. The numbers are also called Euler's idoneal numbers or suitable numbers.
) guarantees it to be a prime, prime power, or twice one of these. The numbers are also called Euler's idoneal numbers or suitable numbers.
A positive integer 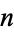 is idoneal iff it cannot be written as
is idoneal iff it cannot be written as 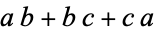 for integer
for integer 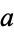 ,
, 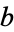 , and
, and 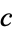 with
with 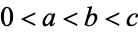 .
.
The 65 idoneal numbers found by Gauss and Euler and conjectured to be the only such numbers (Shanks 1969) are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 15, 16, 18, 21, 22, 24, 25, 28, 30, 33, 37, 40, 42, 45, 48, 57, 58, 60, 70, 72, 78, 85, 88, 93, 102, 105, 112, 120, 130, 133, 165, 168, 177, 190, 210, 232, 240, 253, 273, 280, 312, 330, 345, 357, 385, 408, 462, 520, 760, 840, 1320, 1365, and 1848 (OEIS A000926). It is known that if any other idoneal numbers exist, there can be only one more.
REFERENCES:
Borevich, Z. I. and Shafarevich, I. R. Number Theory. New York: Academic Press, pp. 425-430, 1966.
Cox, D. "Primes of Form 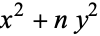 ." New York: Wiley, p. 61, 1989.
." New York: Wiley, p. 61, 1989.
Frei, G. "Euler's Convenient Numbers." Math. Intell. 7, 55-58 and 64, 1985.
Keller, O.-H. "Über die 'Numeri idonei' von Euler." Beiträge Algebra Geom. 16, 79-91, 1983.
Mathews, G, B. Theory of Numbers. Chelsea, p. 263.
Ribenboim, P. "Galimatias Arithmeticae." Math. Mag. 71, 339, 1998.
Ribenboim, P. Ch. 11 in My Numbers, My Friends. New York: Springer-Verlag, 2000.
Shanks, D. "On Gauss's Class Number Problems." Math. Comput. 23, 151-163, 1969.
Sloane, N. J. A. Sequence A000926/M0476 in "The On-Line Encyclopedia of Integer Sequences."
Steinig, J. "On Euler's Idoneal Numbers." Elemente Math. 21, 73-88, 1966.
Weil, A. Number Theory: an Approach Through History, from Hammurapi to Legendre. Boston: Birkhäuser, p. 188, 1984.
Weinberger, P. "Exponents of the Class Groups of Complex Quadratic Fields.' Acta Arith. 22, 117-124, 1973.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|