


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-2-2020
Date: 4-5-2020
Date: 9-11-2020
|
The 2-1 equation
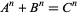 |
(1) |
is a special case of Fermat's last theorem and so has no solutions for 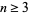 . Lander et al. (1967) give a table showing the smallest
. Lander et al. (1967) give a table showing the smallest 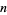 for which a solution to
for which a solution to
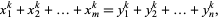 |
(2) |
with 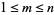 is known. An updated table is given below; a more extensive table may be found at Meyrignac's web site.
is known. An updated table is given below; a more extensive table may be found at Meyrignac's web site.
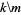 |
1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 2 | |||||
| 3 | 3 | 2 | ||||
| 4 | 3 | 2 | ||||
| 5 | 4 | 3 | ||||
| 6 | 7 | 5 | 3 | |||
| 7 | 7 | 6 | 5 | 4 | ||
| 8 | 8 | 7 | 5 | 5 | ||
| 9 | 10 | 9 | 8 | 6 | 5 | |
| 10 | 13 | 12 | 11 | 9 | 7 | 6 |
Take the results from the Ramanujan 6-10-8 identity that for 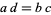 , with
, with
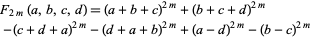 |
(3) |
and
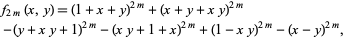 |
(4) |
then
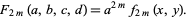 |
(5) |
Using
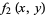 |
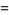 |
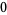 |
(6) |
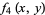 |
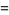 |
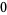 |
(7) |
now gives
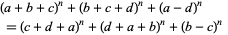 |
(8) |
for 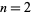 or 4.
or 4.
REFERENCES:
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, p. 101, 1994.
Berndt, B. C. and Bhargava, S. "Ramanujan--For Lowbrows." Amer. Math. Monthly 100, 644-656, 1993.
Dickson, L. E. History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Dover, pp. 653-657, 2005.
Gloden, A. Mehrgradige Gleichungen. Groningen, Netherlands: P. Noordhoff, 1944.
Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, 1994.
Lander, L. J.; Parkin, T. R.; and Selfridge, J. L. "A Survey of Equal Sums of Like Powers." Math. Comput. 21, 446-459, 1967.
Meyrignac, J.-C. "Computing Minimal Equal Sums of Like Powers." https://euler.free.fr.
Reznick, B. Sums of Even Powers of Real Linear Forms. Providence, RI: Amer. Math. Soc., 1992.
Sekigawa, H. and Koyama, K. "Nonexistence Conditions of a Solution for the Congruence 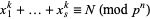 ." Math. Comput. 68, 1283-1297, 1999.
." Math. Comput. 68, 1283-1297, 1999.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|