Square triangle picking is the selection of triples of points (corresponding to endpoints of a triangle) randomly placed inside a square. 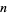 random triangles can be picked in a unit square in the Wolfram Language using the function RandomPoint[Rectangle[], {" src="http://mathworld.wolfram.com/images/equations/SquareTrianglePicking/Inline2.gif" style="height:15px; width:5px" />n, 3}" src="http://mathworld.wolfram.com/images/equations/SquareTrianglePicking/Inline3.gif" style="height:15px; width:5px" />].

Given three points chosen at random inside a unit square, the average area of the triangle determined by these points is given analytically by the multiple integrals

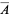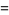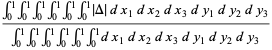			(1)
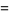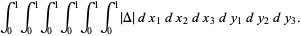			(2)

Here, 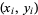 represent the polygon vertices of the triangle for 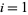, 2, 3, and the (signed) area of these triangles is given by the determinant

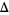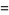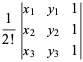			(3)
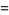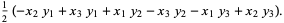			(4)

The solution was first given by Woolhouse (1867). Since attempting to do the integrals by brute force result in intractable integrands, the best approach using computer algebra is to divide the six-dimensional region of integration into subregions using cylindrical algebraic decomposition such that the sign of 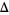 does not change, do the integral in each region directly, and then combine the results (Trott 1998). Depending on the order in which the integration variables are ordered, between 32 and 4168 regions are obtained. The result of combining these pieces gives the mean triangle area

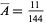(5)

(Ambartzumian 1987, Pfiefer 1989, Trott 1998; Trott 2006, pp. 303-304).

Once 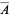 is known, the variance in area is easily calculated by first computing the raw moment ,

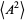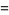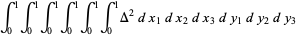			(6)
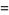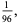			(7)

giving

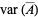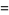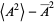			(8)
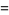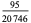			(9)
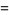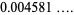			(10)

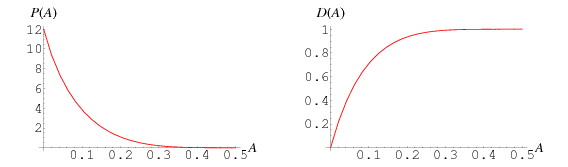
The distribution function for the area of a random triangle inscribed in a square is given exactly by

(11)

(M. Trott, pers. comm., Jan. 27, 2005; Trott 2006, p. 306). The corresponding distribution function is given by

(12)

(Philip).

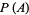 satisfies the beautiful fourth-order ordinary differential equation

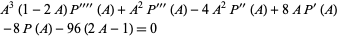(13)

(M. Trott, pers. comm., Jan. 27, 2005; Trott 2006, p. 307).

This gives the beautiful formula for raw moment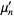s  as

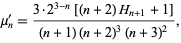(14)

where 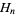 is a harmonic number, so the raw moments for 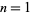, 2, ... are 11/144, 1/96, 137/9000, 1/2400, 363/109760, ... (OEIS A093158 and A093159).

A closed form is more difficult to compute for the 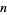th central moments 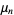, but the first few for 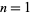, 2, ... are 0, 95/20736, 75979/186624000, 1752451/17915904000, ... (OEIS A103281 and A103282; Trott 2006, p. 307).

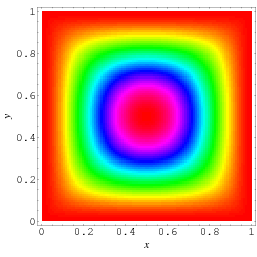
A closed form for the probability that a given point 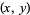 lies within a randomly picked triangle can also be obtained as

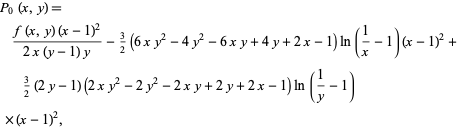(15)

where

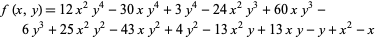(16)

(M. Trott, pers. comm., Jan. 31, 2005; Trott 2006, p. 310). This is expression is valid for 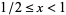 and 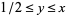, with the expression over the whole unit square given by symmetry as

(17)

As expected, this expression satisfies

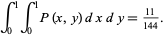(18)

Pick three points at random in the unit square, and denote the probability that the three points form an obtuse triangle by 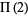. Langford (1969) proved that

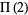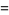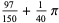			(19)
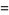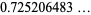			(20)

(OEIS A093072).

REFERENCES:

Alagar, V. S. "On the Distribution of a Random Triangle." J. Appl. Prob. 14, 284-297, 1977.

Ambartzumian, R. V. (Ed.). Stochastic and Integral Geometry. Dordrecht, Netherlands: Reidel, 1987.

Buchta, C. "Über die konvexe Hülle von Zufallspunkten in Eibereichen." Elem. Math. 38, 153-156, 1983.

Buchta, C. "Zufallspolygone in konvexen Vielecken." J. reine angew. Math. 347, 212-220, 1984.

Finch, S. R. "Geometric Probability Constants." §8.1 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 479-484, 2003.

Henze, N. "Random Triangles in Convex Regions." J. Appl. Prob. 20, 111-125, 1983.

Klee, V. "What Is the Expected Volume of a Simplex Whose Vertices Are Chosen at Random from a Given Convex Body." Amer. Math. Monthly 76, 286-288, 1969.

Langford, E. "The Probability that a Random Triangle is Obtuse." Biometrika 56, 689-690, 1969.

Pfiefer, R. E. "The Historical Development of J. J. Sylvester's Four Point Problem." Math. Mag. 62, 309-317, 1989.

Philip, J. "The Area of a Random Convex Polygon." Tech. Report TRITA MAT 04 MA 07. n.d. http://www.math.kth.se/~johanph/area12.pdf.

Santaló, L. A. Integral Geometry and Geometric Probability. Reading, MA: Addison-Wesley, 1976.

Seidov, Z. F. "Letters: Random Triangle." Mathematica J. 7, 414, 2000.

Seidov, Z. F. 2000. http://axchiv.org/abs/math.GM/0002134/.

Sloane, N. J. A. Sequences A093072, A093158, A093159, A103281, and A103282 in "The On-Line Encyclopedia of Integer Sequences."

Trott, M. "The Area of a Random Triangle." Mathematica J. 7, 189-198, 1998. http://library.wolfram.com/infocenter/Articles/3413/.

Trott, M. "Area of a Random Triangle in a Square." §1.10.1 in The Mathematica GuideBook for Symbolics. New York: Springer-Verlag, pp. 298-311, 2006. http://www.mathematicaguidebooks.org/.

Woolhouse, W. S. B. "Question 2471." Mathematical Questions, with Their Solutions, from the Educational Times, Vol. 8. London: F. Hodgson and Son, pp. 100-105, 1867.

اخر الاخبار

اخبار العتبة العباسية المقدسة

جمعية كشافة الكفيل: المجالس الحسينية تعلّم الفتية قيم نهضة الإمام الحسين (عليه السلام)

عَبرَ المجالس الحسينية.. المجمَع العلمي يقدّم محاضرات دينية وتلاوات قرآنية في بغداد والنجف وميسان

برعاية العتبة العباسية المقدسة.. موكب قناديل السماء يُحيي مراسم اليوم الثالث عشر من المحرّم

بعد انتهاء مراسم ذكرى دفن الأجساد الطاهرة قسم رعاية الصحن يباشر بحملة تنظيف واسعة لصحن مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

لكبح الجوع وخسارة الوزن.. "سر بسيط" في نظام جوكوفيتش ؟

هل يساعد الرجيم في علاج الأمراض العقلية؟

لحماية أسنان طفلك.. هذا الفيتامين يقلل خطر التسوس

أكل الطعام بسرعة.. طريق سريع إلى أمراض خطيرة

المزيد

الآخبار التكنلوجية

ما هي أفضل درجة حرارة لتكييف الهواء في السيارة؟

ذوبان الأنهار الجليدية يوقظ "عمالقة نائمة"!

9 يوليو يشهد أقصر يوم في التاريخ المسجل ؟!!

راتبه عشرات ملايين الدولارات.. زوكربرغ يخطف "عقل أبل"

المزيد