Diophantine Equation--5th Powers
The 5.1.2 fifth-order Diophantine equation
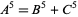 |
(1)
|
is a special case of Fermat's last theorem with 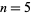 , and so has no solution. improving on the results on Lander et al. (1967), who checked up to
, and so has no solution. improving on the results on Lander et al. (1967), who checked up to 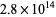 . (In fact, no solutions are known for powers of 6 or 7 either.) No solutions to the 5.1.3 equation
. (In fact, no solutions are known for powers of 6 or 7 either.) No solutions to the 5.1.3 equation
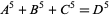 |
(2)
|
are known (Lander et al. 1967). For 4 fifth powers, the 5.1.4 equation has solutions
(Lander and Parkin 1967, Lander et al. 1967, Ekl 1998), the second of which was found by J. Frye (J.-C. Meyrignac, pers. comm., Sep. 9, 2004), but it is not known if there is a parametric solution (Guy 1994, p. 140). Sastry (1934) found a 2-parameter solution for 5.1.5 equations
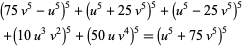 |
(5)
|
(quoted in Lander and Parkin 1967), and Lander and Parkin (1967) found the smallest numerical solutions. Lander et al. (1967) give a list of the smallest solutions, the first few being
(Lander and Parkin 1967, Lander et al. 1967). The 5.1.6 equation has solutions
(Martin 1887, 1888, Lander and Parkin 1967, Lander et al. 1967). The smallest 5.1.7 solution is
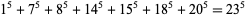 |
(26)
|
(Lander et al. 1967).
No solutions to the 5.2.2 equation
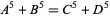 |
(27)
|
are known, despite the fact that sums up to 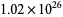 have been checked (Guy 1994, p. 140). The smallest 5.2.3 solution is
have been checked (Guy 1994, p. 140). The smallest 5.2.3 solution is
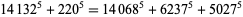 |
(28)
|
(B. Scher and E. Seidl 1996, Ekl 1998). Sastry's (1934) 5.1.5 solution gives some 5.2.4 solutions. The smallest primitive 5.2.4 solutions are
(Rao 1934, Moessner 1948, Lander et al. 1967). The smallest primitive 5.2.5 solutions are
(Rao 1934, Lander et al. 1967).
Parametric solutions are known for the 5.3.3 (Sastry and Lander 1934; Moessner 1951; Swinnerton-Dyer 1952; Lander 1968; Bremmer 1981; Guy 1994, pp. 140 and 142; Choudhry 1999). Swinnerton-Dyer (1952) gave two parametric solutions to the 5.3.3 equation but, forty years later, W. Gosper discovered that the second scheme has an unfixable bug. Choudhry (1999) gave a parametric solution to the more general equation
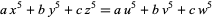 |
(45)
|
with 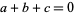 . The smallest primitive solutions to the 5.3.3 equation with unit coefficients are
. The smallest primitive solutions to the 5.3.3 equation with unit coefficients are
(Moessner 1939, Moessner 1948, Lander et al. 1967, Ekl 1998).
A two-parameter solution to the 5.3.4 equation was given by Xeroudakes and Moessner (1958). Gloden (1949) also gave a parametric solution. The smallest solution is
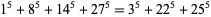 |
(51)
|
(Rao 1934, Lander et al. 1967).
Several parametric solutions to the 5.4.4 equation were found by Xeroudakes and Moessner (1958).
The smallest 5.4.4 solution is
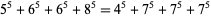 |
(52)
|
(Rao 1934, Lander et al. 1967). The first 5.4.4.4 equation is
(Lander et al. 1967).
Moessner and Gloden (1944) give the 5.5.6 solution
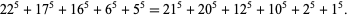 |
(55)
|
Chen Shuwen found the 5.6.6 solution
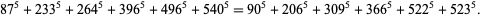 |
(56)
|
REFERENCES:
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, p. 95, 1994.
Bremner, A. "A Geometric Approach to Equal Sums of Fifth Powers." J. Number Th. 13, 337-354, 1981.
Choudhry, A. "The Diophantine Equation 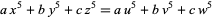 ." Rocky Mtn. J. Math. 29, 459-462, 1999.
." Rocky Mtn. J. Math. 29, 459-462, 1999.
Dutch, S. "Sums of Fifth and Higher Powers." https://www.uwgb.edu/dutchs/RECMATH/rmpowers.htm#5power.
Ekl, R. L. "New Results in Equal Sums of Like Powers." Math. Comput. 67, 1309-1315, 1998.
Gloden, A. "Über mehrgeradige Gleichungen." Arch. Math. 1, 482-483, 1949.
Guy, R. K. "Sums of Like Powers. Euler's Conjecture." §D1 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 139-144, 1994.
Lander, L. J. "Geometric Aspects of Diophantine Equations Involving Equal Sums of Like Power." Amer. Math. Monthly 75, 1061-1073, 1968.
Lander, L. J. and Parkin, T. R. "A Counterexample to Euler's Sum of Powers Conjecture." Math. Comput. 21, 101-103, 1967.
Lander, L. J.; Parkin, T. R.; and Selfridge, J. L. "A Survey of Equal Sums of Like Powers." Math. Comput. 21, 446-459, 1967.
Martin, A. "Methods of Finding 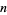 th-Power Numbers Whose Sum is an
th-Power Numbers Whose Sum is an 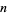 th Power; With Examples." Bull. Philos. Soc. Washington 10, 107-110, 1887.
th Power; With Examples." Bull. Philos. Soc. Washington 10, 107-110, 1887.
Martin, A. Smithsonian Misc. Coll. 33, 1888.
Martin, A. "About Fifth-Power Numbers whose Sum is a Fifth Power." Math. Mag. 2, 201-208, 1896.
Meyrignac, J.-C. "Computing Minimal Equal Sums of Like Powers." https://euler.free.fr.
Moessner, A. "Einige numerische Identitäten." Proc. Indian Acad. Sci. Sect. A 10, 296-306, 1939.
Moessner, A. "Alcune richerche di teoria dei numeri e problemi diofantei." Bol. Soc. Mat. Mexicana 2, 36-39, 1948.
Moessner, A. "Due Sistemi Diofantei." Boll. Un. Mat. Ital. 6, 117-118, 1951.
Moessner, A. and Gloden, A. "Einige Zahlentheoretische Untersuchungen und Resultate." Bull. Sci. École Polytech. de Timisoara 11, 196-219, 1944.
Rao, K. S. "On Sums of Fifth Powers." J. London Math. Soc. 9, 170-171, 1934.
Sastry, S. and Chowla, S. "On Sums of Powers." J. London Math. Soc. 9, 242-246, 1934.
Swinnerton-Dyer, H. P. F. "A Solution of 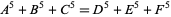 ." Proc. Cambridge Phil. Soc. 48, 516-518, 1952.
." Proc. Cambridge Phil. Soc. 48, 516-518, 1952.
Xeroudakes, G. and Moessner, A. "On Equal Sums of Like Powers." Proc. Indian Acad. Sci. Sect. A 48, 245-255, 1958.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


