

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Diophantine Equation--4th Powers
المؤلف:
Barbette, E
المصدر:
Les sommes de p-iémes puissances distinctes égales à une p-iéme puissance. Doctoral Dissertation, Liege, Belgium. Paris: Gauthier-Villars, 1910.
الجزء والصفحة:
...
20-5-2020
1497
Diophantine Equation--4th Powers
As a consequence of Matiyasevich's refutation of Hilbert's 10th problem, it can be proved that there does not exist a general algorithm for solving a general quartic Diophantine equation. However, the algorithm for constructing such an unsolvable quartic Diophantine equation can require arbitrarily many variables (Matiyasevich 1993).
As a part of the study of Waring's problem, it is known that every positive integer is a sum of no more than 19 positive biquadrates (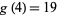 ), that every "sufficiently large" integer is a sum of no more than 16 positive biquadrates (
), that every "sufficiently large" integer is a sum of no more than 16 positive biquadrates (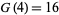 ), and that every integer is a sum of at most 10 signed biquadrates (
), and that every integer is a sum of at most 10 signed biquadrates (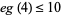 ; although it is not known if 10 can be reduced to 9). The first few numbers
; although it is not known if 10 can be reduced to 9). The first few numbers 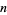 which are a sum of four fourth powers (
which are a sum of four fourth powers (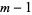 equations) are 353, 651, 2487, 2501, 2829, ... (OEIS A003294).
equations) are 353, 651, 2487, 2501, 2829, ... (OEIS A003294).
The 4.1.2 equation
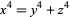 |
(1) |
is a case of Fermat's last theorem with 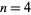 and therefore has no solutions. In fact, the equations
and therefore has no solutions. In fact, the equations
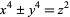 |
(2) |
also have no solutions in integers (Nagell 1951, pp. 227 and 229). The equation
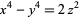 |
(3) |
has no solutions in integers (Nagell 1951, p. 230). The only number of the form
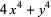 |
(4) |
which is prime is 5 (Baudran 1885, Le Lionnais 1983).
Let the notation 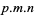 stand for the equation consisting of a sum of
stand for the equation consisting of a sum of 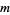
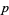 th powers being equal to a sum of
th powers being equal to a sum of 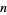
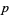 th powers. In 1772, Euler proposed that the 4.1.3 equation
th powers. In 1772, Euler proposed that the 4.1.3 equation
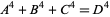 |
(5) |
had no solutions in integers (Lander et al. 1967). This assertion is known as the Euler quartic conjecture. Ward (1948) showed there were no solutions for 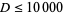 , which was subsequently improved to
, which was subsequently improved to 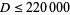 by Lander et al. (1967). However, the Euler quartic conjecture was disproved in 1987 by N. Elkies, who, using a geometric construction, found
by Lander et al. (1967). However, the Euler quartic conjecture was disproved in 1987 by N. Elkies, who, using a geometric construction, found
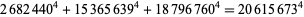 |
(6) |
and showed that infinitely many solutions existed (Guy 1994, p. 140). In 1988, Roger Frye found
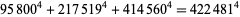 |
(7) |
and proved that there are no solutions in smaller integers (Guy 1994, p. 140). Another solution was found by Allan MacLeod in 1997,
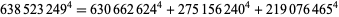 |
(8) |
(Ekl 1998). It is not known if there is a parametric solution. In contrast, there are many solutions to the equation
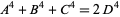 |
(9) |
(see below).
The 4.1.4 equation
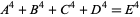 |
(10) |
has solutions
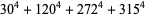 |
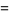 |
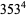 |
(11) |
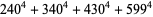 |
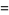 |
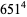 |
(12) |
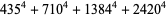 |
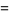 |
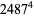 |
(13) |
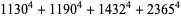 |
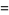 |
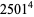 |
(14) |
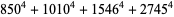 |
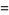 |
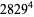 |
(15) |
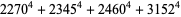 |
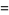 |
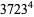 |
(16) |
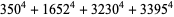 |
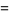 |
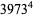 |
(17) |
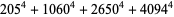 |
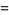 |
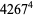 |
(18) |
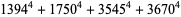 |
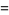 |
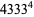 |
(19) |
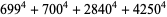 |
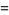 |
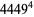 |
(20) |
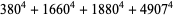 |
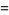 |
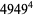 |
(21) |
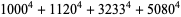 |
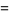 |
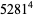 |
(22) |
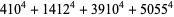 |
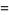 |
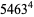 |
(23) |
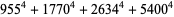 |
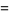 |
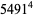 |
(24) |
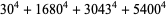 |
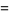 |
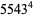 |
(25) |
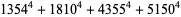 |
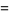 |
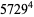 |
(26) |
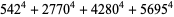 |
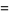 |
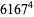 |
(27) |
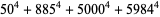 |
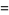 |
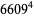 |
(28) |
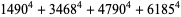 |
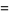 |
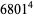 |
(29) |
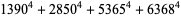 |
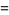 |
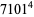 |
(30) |
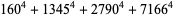 |
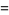 |
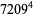 |
(31) |
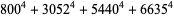 |
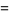 |
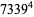 |
(32) |
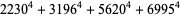 |
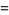 |
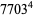 |
(33) |
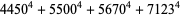 |
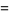 |
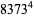 |
(34) |
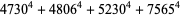 |
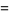 |
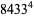 |
(35) |
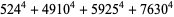 |
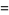 |
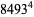 |
(36) |
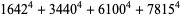 |
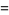 |
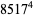 |
(37) |
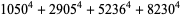 |
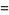 |
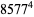 |
(38) |
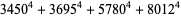 |
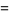 |
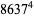 |
(39) |
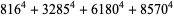 |
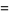 |
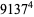 |
(40) |
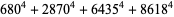 |
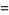 |
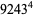 |
(41) |
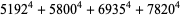 |
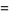 |
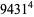 |
(42) |
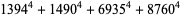 |
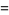 |
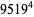 |
(43) |
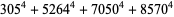 |
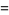 |
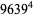 |
(44) |
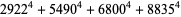 |
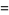 |
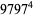 |
(45) |
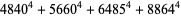 |
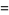 |
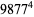 |
(46) |
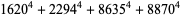 |
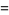 |
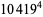 |
(47) |
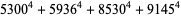 |
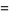 |
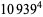 |
(48) |
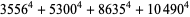 |
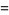 |
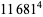 |
(49) |
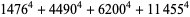 |
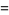 |
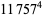 |
(50) |
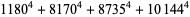 |
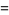 |
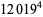 |
(51) |
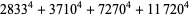 |
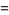 |
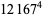 |
(52) |
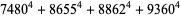 |
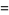 |
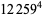 |
(53) |
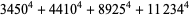 |
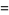 |
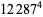 |
(54) |
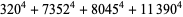 |
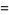 |
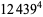 |
(55) |
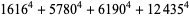 |
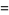 |
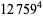 |
(56) |
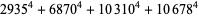 |
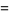 |
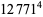 |
(57) |
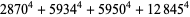 |
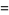 |
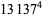 |
(58) |
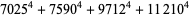 |
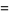 |
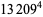 |
(59) |
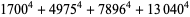 |
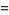 |
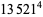 |
(60) |
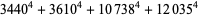 |
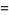 |
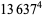 |
(61) |
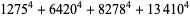 |
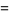 |
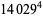 |
(62) |
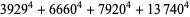 |
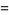 |
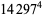 |
(63) |
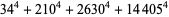 |
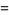 |
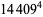 |
(64) |
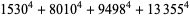 |
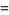 |
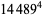 |
(65) |
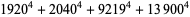 |
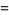 |
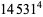 |
(66) |
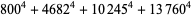 |
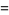 |
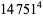 |
(67) |
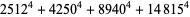 |
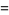 |
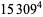 |
(68) |
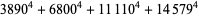 |
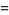 |
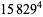 |
(69) |
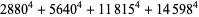 |
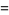 |
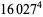 |
(70) |
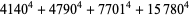 |
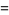 |
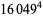 |
(71) |
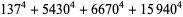 |
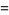 |
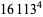 |
(72) |
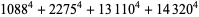 |
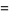 |
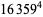 |
(73) |
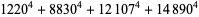 |
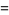 |
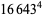 |
(74) |
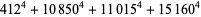 |
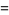 |
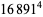 |
(75) |
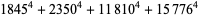 |
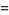 |
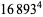 |
(76) |
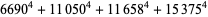 |
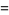 |
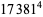 |
(77) |
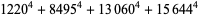 |
 |
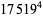 |
(78) |
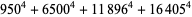 |
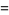 |
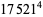 |
(79) |
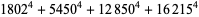 |
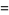 |
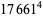 |
(80) |
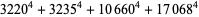 |
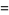 |
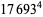 |
(81) |
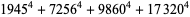 |
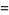 |
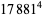 |
(82) |
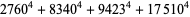 |
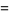 |
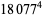 |
(83) |
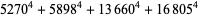 |
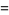 |
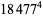 |
(84) |
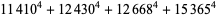 |
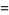 |
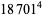 |
(85) |
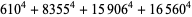 |
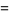 |
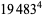 |
(86) |
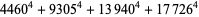 |
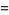 |
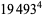 |
(87) |
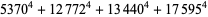 |
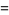 |
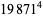 |
(88) |
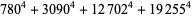 |
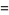 |
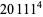 |
(89) |
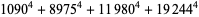 |
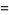 |
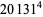 |
(90) |
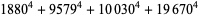 |
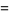 |
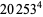 |
(91) |
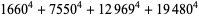 |
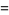 |
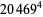 |
(92) |
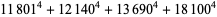 |
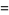 |
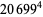 |
(93) |
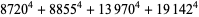 |
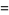 |
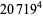 |
(94) |
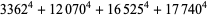 |
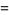 |
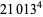 |
(95) |
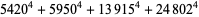 |
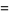 |
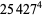 |
(96) |
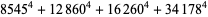 |
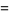 |
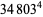 |
(97) |
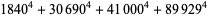 |
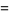 |
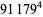 |
(98) |
(Norrie 1911, Patterson 1942, Leech 1958, Brudno 1964, Lander et al. 1967, Rose and Brudno 1973; A. Stinchcombe, pers. comm., Oct. 25, 2004). Additional solution are given by Wroblewski.
It was not known if there was a parametric solution (Guy 1994, p. 139) until Jacobi and Madden (2008) found an infinite number of solutions to the special case
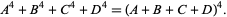 |
(99) |
Their solution makes extensive use of elliptic curve theory and the special solution (955, 1770, 2634, 5400; 5491) due to Brudno (1964), which satisfies 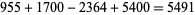 .
.
There are an infinite number of solutions to the 4.1.5 equation
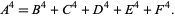 |
(100) |
Some of the smallest are
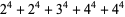 |
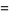 |
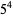 |
(101) |
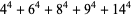 |
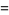 |
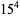 |
(102) |
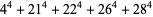 |
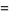 |
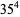 |
(103) |
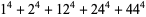 |
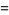 |
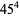 |
(104) |
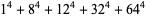 |
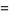 |
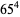 |
(105) |
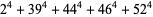 |
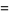 |
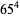 |
(106) |
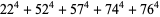 |
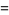 |
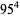 |
(107) |
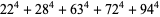 |
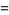 |
 |
(108) |
(Berndt 1994). Berndt and Bhargava (1993) and Berndt (1994, pp. 94-96) give Ramanujan's solutions for arbitrary 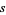 ,
, 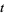 ,
, 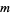 , and
, and 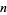 ,
,
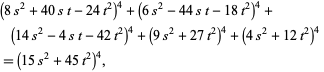 |
(109) |
and
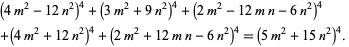 |
(110) |
These are also given by Dickson (2005, p. 649), and two general formulas are given by Beiler (1966, p. 290). Other solutions are given by Fauquembergue (1898), Haldeman (1904), and Martin (1910). Similar quadratic form parametrizations given by Ramanujan can be found using the identity
![[ax^2+2(b+c)xy-3ay^2]^k+[bx^2-2(a+c)xy-3by^2]^k+[cx^2-2(a-b)xy-3cy^2]^k=(a^k+b^k+c^k)(x^2+3y^2)^k,](https://mathworld.wolfram.com/images/equations/DiophantineEquation4thPowers/NumberedEquation15.gif) |
(111) |
where 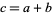 for
for 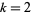 or 4, though this is just a special case of an even more general identity (Piezas 2005). The situation is then reduced to finding solutions to
or 4, though this is just a special case of an even more general identity (Piezas 2005). The situation is then reduced to finding solutions to 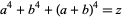 , where
, where 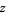 is the sum and difference of a number of fourth powers. As an example, given
is the sum and difference of a number of fourth powers. As an example, given
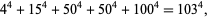 |
(112) |
then
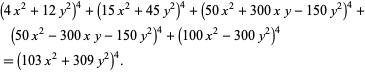 |
(113) |
Similarly, given the identity and the equation
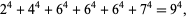 |
(114) |
then there are an infinite number of primitive solutions to the 4.1.6 equation.
Parametric solutions to the 4.2.2 equation
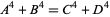 |
(115) |
are known (Euler 1802; Gérardin 1917; Guy 1994, pp. 140-141), but no "general" solution is known (Hardy 1999, p. 21). The first few primitive solutions are
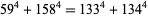 |
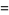 |
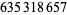 |
(116) |
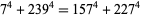 |
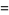 |
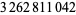 |
(117) |
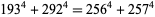 |
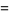 |
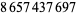 |
(118) |
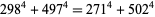 |
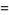 |
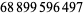 |
(119) |
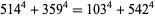 |
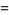 |
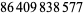 |
(120) |
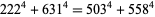 |
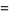 |
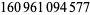 |
(121) |
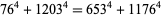 |
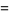 |
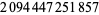 |
(122) |
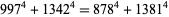 |
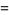 |
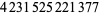 |
(123) |
(OEIS A003824; Richmond 1920; Dickson 1957, pp. 60-62; Leech 1957; Berndt 1994, p. 107; Ekl 1998 [with typo]; Dickson 2005, pp. 644-647), the smallest of which is due to Euler (Hardy 1999, p. 21). Lander et al. (1967) give a list of 25 primitive 4.2.2 solutions. General (but incomplete) solutions are given by
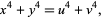 |
(124) |
where
 |
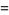 |
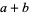 |
(125) |
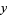 |
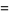 |
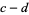 |
(126) |
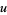 |
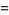 |
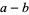 |
(127) |
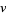 |
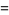 |
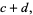 |
(128) |
and
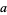 |
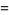 |
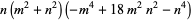 |
(129) |
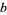 |
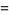 |
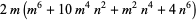 |
(130) |
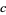 |
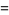 |
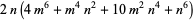 |
(131) |
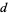 |
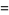 |
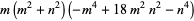 |
(132) |
(Hardy and Wright 1979).
Parametric solutions to the 4.2.3 equation
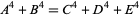 |
(133) |
are known (Gérardin 1910, Ferrari 1913). The smallest solution is
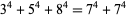 |
(134) |
(Lander et al. 1967).
Ramanujan gave the 4.2.4 equation
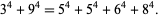 |
(135) |
Ramanujan gave the 4.3.3 equations
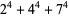 |
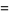 |
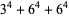 |
(136) |
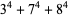 |
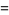 |
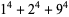 |
(137) |
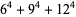 |
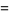 |
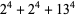 |
(138) |
(Berndt 1994, p. 101). Similar examples can be found in Martin (1896). Parametric solutions were given by Gérardin (1911).
Ramanujan also gave the general expression
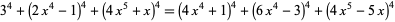 |
(139) |
(Berndt 1994, p. 106). Dickson (2005, pp. 653-655) cites several formulas giving solutions to the 4.3.3 equation, and Haldeman (1904) gives a general formula.
Ramanujan gave the 4.3.4 identities
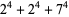 |
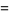 |
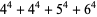 |
(140) |
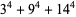 |
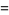 |
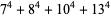 |
(141) |
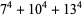 |
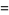 |
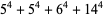 |
(142) |
(Berndt 1994, p. 101). Haldeman (1904) gives general formulas for 4-2 and 4-3 equations.
Ramanujan gave
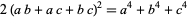 |
(143) |
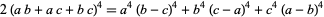 |
(144) |
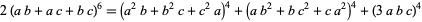 |
(145) |
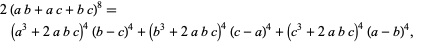 |
(146) |
where
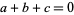 |
(147) |
(Berndt 1994, pp. 96-97). Formula (◇) is equivalent to Ferrari's identity
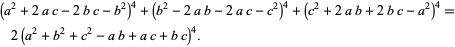 |
(148) |
Bhargava's theorem is a general identity which gives the above equations as a special case, and may have been the route by which Ramanujan proceeded. Another identity due to Ramanujan is
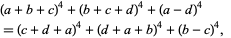 |
(149) |
where 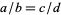 , and 4 may also be replaced by 2 (Ramanujan 1987, Hirschhorn 1998).
, and 4 may also be replaced by 2 (Ramanujan 1987, Hirschhorn 1998).
V. Kyrtatas (pers. comm., June 19, 1997) noticed that 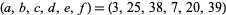 satisfy
satisfy
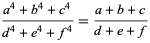 |
(150) |
and asked if there are any other distinct integer solutions. Additional solutions are (285, 2964, 3249, 1769, 1952, 3721) and (185, 1184, 1369, 663, 858, 1521) (E. Clark, pers. comm., Jan. 26, 2004) and (5160, 11481, 16641, 3683, 12446, 16129), (7367, 11954, 19321, 2660, 15029, 17689) (14925, 24676, 39601, 7527, 29722, 37249), (7136, 42593, 49729, 2387, 44702, 47089) (A. Stinchcombe, pers. comm., Nov. 19, 2004).
REFERENCES:
Barbette, E. Les sommes de 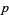 -iémes puissances distinctes égales à une p-iéme puissance. Doctoral Dissertation, Liege, Belgium. Paris: Gauthier-Villars, 1910.
-iémes puissances distinctes égales à une p-iéme puissance. Doctoral Dissertation, Liege, Belgium. Paris: Gauthier-Villars, 1910.
Beiler, A. H. Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, 1966.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, 1994.
Berndt, B. C. and Bhargava, S. "Ramanujan--For Lowbrows." Am. Math. Monthly 100, 645-656, 1993.
Bhargava, S. "On a Family of Ramanujan's Formulas for Sums of Fourth Powers." Ganita 43, 63-67, 1992.
Brudno, S. "A Further Example of 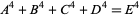 ." Proc. Cambridge Phil. Soc. 60, 1027-1028, 1964.
." Proc. Cambridge Phil. Soc. 60, 1027-1028, 1964.
Dickson, L. E. Introduction to the Theory of Numbers. New York: Dover, 1957.
Dickson, L. E. History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Dover, 2005.
Dutch, S. "Power Page: Sums of Fourth Powers." https://www.uwgb.edu/dutchs/RECMATH/rmpowers.htm#4power.
Ekl, R. L. "New Results in Equal Sums of Like Powers." Math. Comput. 67, 1309-1315, 1998.
Euler, L. Nova Acta Acad. Petrop. as annos 1795-1796 13, 45, 1802.
Fauquembergue, E. L'intermédiaire des Math. 5, 33, 1898.
Ferrari, F. L'intermédiaire des Math. 20, 105-106, 1913.
Guy, R. K. "Sums of Like Powers. Euler's Conjecture" and "Some Quartic Equations." §D1 and D23 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 139-144 and 192-193, 1994.
Haldeman, C. B. "On Biquadrate Numbers." Math. Mag. 2, 285-296, 1904.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Hardy, G. H. and Wright, E. M. §13.7 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Hirschhorn, M. D. "Two or Three Identities of Ramanujan." Amer. Math. Monthly 105, 52-55, 1998.
Jacobi, L. W. and Madden D. J. "On 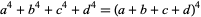 ." Amer. Math. Monthly 115, 220-236, 2008.
." Amer. Math. Monthly 115, 220-236, 2008.
Lander, L. J.; Parkin, T. R.; and Selfridge, J. L. "A Survey of Equal Sums of Like Powers." Math. Comput. 21, 446-459, 1967.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 56, 1983.
Leech, J. "Some Solutions of Diophantine Equations." Proc. Cambridge Phil. Soc. 53, 778-780, 1957.
Leech, J. "On 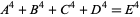 ." Proc. Cambridge Phil. Soc. 54, 554-555, 1958.
." Proc. Cambridge Phil. Soc. 54, 554-555, 1958.
Martin, A. "About Biquadrate Numbers whose Sum is a Biquadrate." Math. Mag. 2, 173-184, 1896.
Martin, A. "About Biquadrate Numbers whose Sum is a Biquadrate--II." Math. Mag. 2, 325-352, 1904.
Matiyasevich, Yu. V. Hilbert's Tenth Problem. Cambridge, MA: MIT Press, 1993. https://www.informatik.uni-stuttgart.de/ifi/ti/personen/Matiyasevich/H10Pbook/.
Meyrignac, J.-C. "Computing Minimal Equal Sums of Like Powers." https://euler.free.fr.
Nagell, T. "Some Diophantine Equations of the Fourth Degree with Three Unknowns" and "The Diophantine Equation 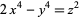 ." §62 and 63 in Introduction to Number Theory. New York: Wiley, pp. 227-235, 1951.
." §62 and 63 in Introduction to Number Theory. New York: Wiley, pp. 227-235, 1951.
Norrie, R. University of St. Andrews 500th Anniversary Memorial Volume. Edinburgh, Scotland: pp. 87-89, 1911.
Patterson, J. O. "A Note on the Diophantine Problem of Finding Four Biquadrates whose Sum is a Biquadrate." Bull. Amer. Math. Soc. 48, 736-737, 1942.
Piezas, T. "Ramanujan and the Quartic Equation 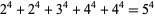 ." 2005. https://www.geocities.com/titus_piezas/RamQuad.pdf.
." 2005. https://www.geocities.com/titus_piezas/RamQuad.pdf.
Ramanujan, S. Notebooks. New York: Springer-Verlag, pp. 385-386, 1987.
Richmond, H. W. "On Integers Which Satisfy the Equation 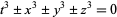 ." Trans. Cambridge Phil. Soc. 22, 389-403, 1920.
." Trans. Cambridge Phil. Soc. 22, 389-403, 1920.
Rivera, C. "Problems & Puzzles: Puzzle 047-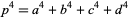 ,
, 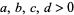 ." https://www.primepuzzles.net/puzzles/puzz_047.htm.
." https://www.primepuzzles.net/puzzles/puzz_047.htm.
Rose, K. and Brudno, S. "More About Four Biquadrates Equal One Biquadrate." Math. Comput. 27, 491-494, 1973.
Science Daily. "Mathematicians Find New Solutions to an Ancient Puzzle." March 18, 2008. https://www.sciencedaily.com/releases/2008/03/080314145039.htm.
Sloane, N. J. A. Sequences A003294/M5446, A003824, and A018786 in "The On-Line Encyclopedia of Integer Sequences."
Ward, M. "Euler's Problem on Sums of Three Fourth Powers." Duke Math. J. 15, 827-837, 1948.
Wroblewski, J. "Equal Sums and Differences of 4th Powers." https://www.math.uni.wroc.pl/~jwr/eslp/414.txt.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















