A Diophantine equation is an equation in which only integer solutions are allowed.

Hilbert's 10th problem asked if an algorithm existed for determining whether an arbitrary Diophantine equation has a solution. Such an algorithm does exist for the solution of first-order Diophantine equations. However, the impossibility of obtaining a general solution was proven by Yuri Matiyasevich in 1970 (Matiyasevich 1970, Davis 1973, Davis and Hersh 1973, Davis 1982, Matiyasevich 1993) by showing that the relation 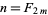 (where  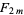is the 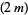th Fibonacci number) is Diophantine. More specifically, Matiyasevich showed that there is a polynomial  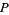in 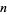, , 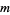and a number of other variables , , 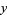, 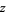... having the property that  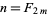iff there exist integers , , 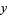, 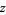... such that .

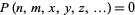Matiyasevich's result filled a crucial gap in previous work by Martin Davis, Hilary Putnam, and Julia Robinson. Subsequent work by Matiyasevich and Robinson proved that even for equations in thirteen variables, no algorithm can exist to determine whether there is a solution. Matiyasevich then improved this result to equations in only nine variables (Jones and Matiyasevich 1982).

Ogilvy and Anderson (1988) give a number of Diophantine equations with known and unknown solutions.

A linear Diophantine equation (in two variables) is an equation of the general form

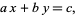(1)

where solutions are sought with 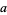, , 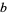and 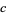 integers. Such equations can be solved completely, and the first known solution was constructed by Brahmagupta. Consider the equation

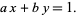(2)

Now use a variation of the Euclidean algorithm, letting 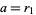 and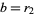 

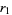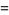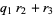			(3)
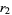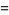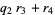			(4)
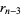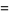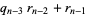			(5)
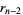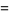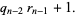			(6)

Starting from the bottom gives

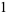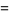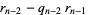			(7)
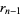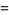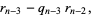			(8)

so

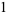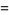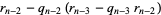			(9)
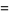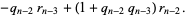			(10)

Continue this procedure all the way back to the top.

Take as an example the equation

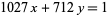(11)

and apply the algorithm above to obtain

(12)

The solution is therefore , .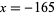

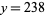The above procedure can be simplified by noting that the two leftmost columns are offset by one entry and alternate signs, as they must since

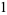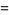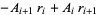			(13)
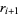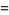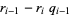			(14)
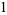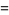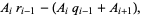			(15)

so the coefficients of 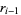 and 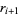 are the same and

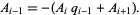(16)

Repeating the above example using this information therefore gives

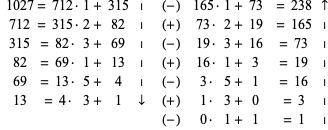(17)

and we recover the above solution.

Call the solutions to

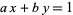(18)

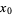 and 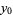. If the signs in front of  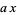or 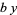 are negative, then solve the above equation and take the signs of the solutions from the following table:

equation

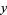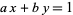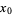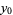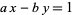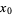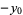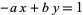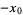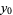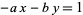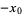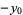In fact, the solution to the equation

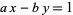(19)

is equivalent to finding the continued fraction for 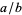, with  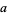and 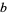 relatively prime (Olds 1963). If there are  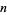terms in the fraction, take the 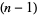th convergen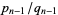t . But

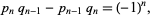(20)

so one solution is 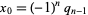, , 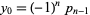with a general solution

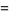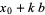			(21)
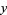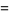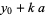			(22)

with 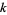 an arbitrary integer. The solution in terms of smallest positive integers is given by choosing an appropriate .

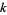Now consider the general first-order equation of the form

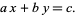(23)

The greatest common divisor 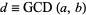 can be divided through yielding

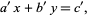(24)

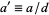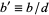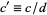where , , and . If 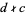, then  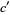is not an integer and the equation cannot have a solution in integers. A necessary and sufficient condition for the general first-order equation to have solutions in integers is therefore that 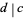. If this is the case, then solve

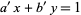(25)

and multiply the solutions by 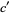, since

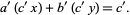(26)

D. Wilson has compiled a list of the smallest 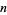th powers of positive integers that are the sums of the 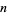th powers of distinct smaller positive integers. The first few are 3, 5, 6, 15, 12, 25, 40, ...(OEIS A030052):

			(27)
			(28)
			(29)
			(30)
			(31)
			(32)
			(33)
			(34)
			(35)
			(36)

REFERENCES:

Alpern, D. "Sums of Powers." https://www.alpertron.com.ar/SUMPOWER.HTM.

Bashmakova, I. G. Diophantus and Diophantine Equations. Washington, DC: Math. Assoc. Amer., 1997.

Beiler, A. H. Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, 1966.

Carmichael, R. D. The Theory of Numbers, and Diophantine Analysis. New York: Dover, 1959.

Courant, R. and Robbins, H. "Continued Fractions. Diophantine Equations." §2.4 in Supplement to Ch. 1 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 49-51, 1996.

Davis, M. "Hilbert's Tenth Problem is Unsolvable." Amer. Math. Monthly 80, 233-269, 1973.

Davis, M. and Hersh, R. "Hilbert's 10th Problem." Sci. Amer. 229, 84-91, Nov. 1973.

Davis, M. "Hilbert's Tenth Problem is Unsolvable." Appendix 2 in Computability and Unsolvability. New York: Dover, 1999-235, 1982.

Dickson, L. E. "Linear Diophantine Equations and Congruences." Ch. 2 in History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Dover, pp. 41-99, 2005.

dmoz. "Equal Sums of Like Powers." https://dmoz.org/Science/Math/Number_Theory/Diophantine_Equations/Equal_Sums_of_Like_Powers/.

Dörrie, H. "The Fermat-Gauss Impossibility Theorem." §21 in 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, pp. 96-104, 1965.

Ekl, R. L. "New Results in Equal Sums of Like Powers." Math. Comput. 67, 1309-1315, 1998.

Guy, R. K. "Diophantine Equations." Ch. D in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 139-198, 1994.

Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.

Hunter, J. A. H. and Madachy, J. S. "Diophantos and All That." Ch. 6 in Mathematical Diversions. New York: Dover, pp. 52-64, 1975.

Ireland, K. and Rosen, M. "Diophantine Equations." Ch. 17 in A Classical Introduction to Modern Number Theory, 2nd ed. New York: Springer-Verlag, pp. 269-296, 1990.

Jones, J. P. and Matiyasevich, Yu. V. "Exponential Diophantine Representation of Recursively Enumerable Sets." Proceedings of the Herbrand Symposium, Marseilles, 1981. Amsterdam, Netherlands: North-Holland, pp. 159-177, 1982.

Lang, S. Introduction to Diophantine Approximations, 2nd ed. New York: Springer-Verlag, 1995.

Matiyasevich, Yu. V. "Solution of the Tenth Problem of Hilbert." Mat. Lapok 21, 83-87, 1970.

Matiyasevich, Yu. V. Hilbert's Tenth Problem. Cambridge, MA: MIT Press, 1993. https://www.informatik.uni-stuttgart.de/ifi/ti/personen/Matiyasevich/H10Pbook/.

Meyrignac, J.-C. "Computing Minimal Equal Sums of Like Powers." https://euler.free.fr/.

Mordell, L. J. Diophantine Equations. New York: Academic Press, 1969.

Nagell, T. "Diophantine Equations of First Degree." §10 in Introduction to Number Theory. New York: Wiley, pp. 29-32, 1951.

Ogilvy, C. S. and Anderson, J. T. "Diophantine Equations." Ch. 6 in Excursions in Number Theory. New York: Dover, pp. 65-83, 1988.

Olds, C. D. Ch. 2 in Continued Fractions. New York: Random House, 1963.

Sloane, N. J. A. Sequence A030052 in "The On-Line Encyclopedia of Integer Sequences."

Weisstein, E. W. "Books about Diophantine Equations." https://www.ericweisstein.com/encyclopedias/books/DiophantineEquations.html.

اخر الاخبار

اخبار العتبة العباسية المقدسة

العتبة العباسية المقدسة تقيم مهرجان إكليل العفة في جامعة كربلاء

في ست محافظات عراقية.. إحياء ذكرى المبعث النبوي الشريف واليوم الوطني للقرآن الكريم

سماحة السيد الصافي يشارك في مراسم تشييع جثمان آية الله السيد هادي السيستاني في النجف

قسم الشؤون الفكرية يصدر كتابًا توثيقيًّا عن جرائم الإرهاب بحق زائري الأربعين في العراق

المزيد

الآخبار الصحية

العلاج بالماء البارد.. باحثون يكشفون فوائده الصحية

من دون صالة رياضية.. عادة بسيطة لتحسين الصحة وخسارة الوزن

لصحة القلب وتفادي السرطان.. استهلك هذا النوع من الطعام

دراسة تحذر من خطر شرب القهوة في أكواب البلاستيك

المزيد

الآخبار التكنلوجية

إنجاز طبي تاريخي.. جراحة قلب بلا شق في الصدر

اليابان.. مراحيض توفر فحص للحالة الصحية عبر "تحليل البراز" !

اختراق واسع لمنصة "إنستغرام".. ونشر بيانات على "الدارك ويب"

علماء يحذرون: هكذا سيفنى كوكب الأرض

المزيد