Archimedes' cattle problem, also called the bovinum problema, or Archimedes' reverse, is stated as follows: "The sun god had a herd of cattle consisting of bulls and cows, one part of which was white, a second black, a third spotted, and a fourth brown. Among the bulls, the number of white ones was one half plus one third the number of the black greater than the brown; the number of the black, one quarter plus one fifth the number of the spotted greater than the brown; the number of the spotted, one sixth and one seventh the number of the white greater than the brown. Among the cows, the number of white ones was one third plus one quarter of the total black cattle; the number of the black, one quarter plus one fifth the total of the spotted cattle; the number of spotted, one fifth plus one sixth the total of the brown cattle; the number of the brown, one sixth plus one seventh the total of the white cattle. What was the composition of the herd?"

Solution consists of solving the simultaneous Diophantine equations in integers 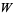, , 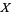,  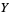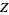(the number of white, black, spotted, and brown bulls) and 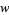, , ,  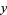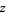(the number of white, black, spotted, and brown cows),

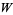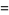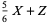			(1)
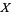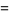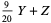			(2)
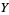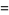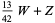			(3)
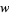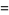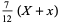			(4)
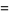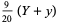			(5)
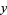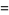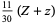			(6)
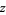			(7)

The smallest solution in integers is

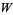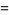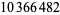			(8)
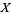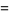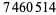			(9)
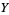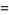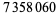			(10)
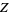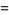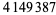			(11)
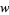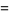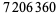			(12)
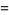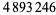			(13)
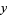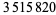			(14)
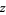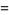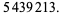			(15)

A more complicated version of the problem requires that 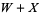 be a square number and  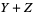a triangular number. The solutions to this problem are numbers with 206544 or 206545 digits, which was first obtained by Williams et al. (1965). Their calculations required 7 hours and 49 minutes of computing time, and the results were deposited in the Unpublished Mathematical Tables file of the Mathematics of Computation journal. Nelson (1980-81) published the 47-page printout from a CRAY 1 computer containing the 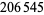-digit solution. These computations, together with checking, took about ten minutes. In addition to the smallest solution, five additional solutions were found to further test the computer, with the largest containing more than one million digits (Rorres). More recently, Vardi (1998) developed simple explicit formulas to generate solutions to the cattle problem. In fact, the solution can (almost) be done out of the box in the Wolfram Language using FindInstance. The total number of cattle is then given by

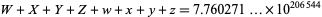(16)

(OEIS A096151).

REFERENCES:

Amthor, A. and Krumbiegel B. "Das Problema bovinum des Archimedes." Z. Math. Phys. 25, 121-171, 1880.

Archibald, R. C. "Cattle Problem of Archimedes." Amer. Math. Monthly 25, 411-414, 1918.

Beiler, A. H. Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, pp. 249-252, 1966.

Bell, A. H. "Solution to the Celebrated Indeterminate Equation 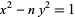." Amer. Math. Monthly 1, 240, 1894.

Bell, A. H. "'Cattle Problem.' By Archimedes 251 BC." Amer. Math. Monthly 2, 140, 1895.

Bell, A. H. "Cattle Problem of Archimedes." Math. Mag. 1, 163, 1882-1884.

Burton, D. M. Elementary Number Theory, 4th ed. Boston, MA: Allyn and Bacon, p. 391, 1989.

Calkins, K. G. "Archimedes' Problema Bovinum." https://www2.andrews.edu/~calkins/profess/cattle.htm.

Dickson, L. E. History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Dover, pp. 342-345, 2005.

Dörrie, H. "Archimedes' Problema Bovinum." §1 in 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, pp. 3-7, 1965.

Drexel University. "The Cattle Problem: Statement." https://www.mcs.drexel.edu/~crorres/Archimedes/Cattle/Statement.html.

Grosjean, C. C. and de Meyer, H. E. "A New Contribution to the Mathematical Study of the Cattle-Problem of Archimedes." In Constantin Carathéodory: An International Tribute, Vols. 1 and 2 (Ed. T. M. Rassias). Teaneck, NJ: World Scientific, pp. 404-453, 1991.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, p. 93, 2003.

Lenstra, H. W. Jr. "Solving the Pell Equation." Not. Amer. Math. Soc. 49, 182-192, 2002.

Merriman, M. "Cattle Problem of Archimedes." Pop. Sci. Monthly 67, 660-665, 1905.

Nelson, H. L. "A Solution to Archimedes' Cattle Problem." J. Recr. Math. 13, 162-176, 1980-81.

Peterson, I. "MathTrek: Cattle of the Sun." April 20, 1998. https://www.maa.org/mathland/mathtrek_4_20_98.html.

Rorres, C. "The Cattle Problem." https://www.mcs.drexel.edu/~crorres/Archimedes/Cattle/Statement.html.

Rorres, C. "The Cattle Problem." https://www.mcs.drexel.edu/~crorres/Archimedes/Cattle/Solution2.html.

Sloane, N. J. A. Sequence A096151 in "The On-Line Encyclopedia of Integer Sequences."

Stewart, I. "Mathematical Recreations: Counting the Cattle of the Sun." Sci. Amer. 282, 112-113, Apr. 2000.

Vardi, I. "Archimedes' Cattle Problem." Amer. Math. Monthly 105, 305-319, 1998.

Williams, H. C.; German, R. A.; and Zarnke, C. R. "Solution of the Cattle Problem of Archimedes." Math. Comput. 19, 671-674, 1965.

Winans, A. "Archimedes' Cattle Problem and Pell's Equation." May 5, 2000. https://www.math.uchicago.edu/~kobotis/media/163/winans.pdf.

اخر الاخبار

اخبار العتبة العباسية المقدسة

جمعية كشافة الكفيل: المجالس الحسينية تعلّم الفتية قيم نهضة الإمام الحسين (عليه السلام)

عَبرَ المجالس الحسينية.. المجمَع العلمي يقدّم محاضرات دينية وتلاوات قرآنية في بغداد والنجف وميسان

برعاية العتبة العباسية المقدسة.. موكب قناديل السماء يُحيي مراسم اليوم الثالث عشر من المحرّم

بعد انتهاء مراسم ذكرى دفن الأجساد الطاهرة قسم رعاية الصحن يباشر بحملة تنظيف واسعة لصحن مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

لكبح الجوع وخسارة الوزن.. "سر بسيط" في نظام جوكوفيتش ؟

هل يساعد الرجيم في علاج الأمراض العقلية؟

لحماية أسنان طفلك.. هذا الفيتامين يقلل خطر التسوس

أكل الطعام بسرعة.. طريق سريع إلى أمراض خطيرة

المزيد

الآخبار التكنلوجية

ما هي أفضل درجة حرارة لتكييف الهواء في السيارة؟

ذوبان الأنهار الجليدية يوقظ "عمالقة نائمة"!

9 يوليو يشهد أقصر يوم في التاريخ المسجل ؟!!

راتبه عشرات ملايين الدولارات.. زوكربرغ يخطف "عقل أبل"

المزيد