المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر المرجع الالكتروني للمعلوماتية
أضيف حديثاً
السيادة القمية Apical Dominance في البطاطس
2024-11-28
مناخ المرتفعات Height Climate
2024-11-28
التربة المناسبة لزراعة البطاطس Solanum tuberosum
2024-11-28
مدى الرؤية Visibility
2024-11-28
Stratification
2024-11-28
استخدامات الطاقة الشمسية Uses of Solar Radiation
2024-11-28

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
باشدو رسام آمون.
2024-07-21
القيم الاساسية او المرجعية Reference values
20-8-2020
مقدمة عن أسباب التغيرات المناخية
16-9-2019
أقسام منهج التفسير الإشاريّ
2024-09-23
الحياة الدينية للعرب قبل الاسلام
7-11-2016
كلام في إقسامه تعالى في القرآن
5-10-2014

Pi Squared  
  
578   03:51 مساءً   date: 10-3-2020
Author : Bailey, D. H.; Borwein, P.; and Plouffe, S.
Book or Source : "On the Rapid Computation of Various Polylogarithmic Constants." Math. Comput. 66
Page and Part : ...


Read More
Cosine
Date: 10-4-2020 2134
Gaussian Brackets
Date: 2-5-2020 661
Truncated Tetrahedral Number
Date: 25-12-2020 859

Pi Squared

There is a series of BBP-type formulas for 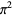pi^2 in powers of (-1)^k,

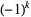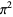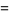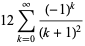pi^2 = 12sum_(k=0)^(infty)((-1)^k)/((k+1)^2)

(1)
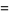= sum_(k=0)^(infty)(-1)^k[(13)/((3k+1)^2)-(13)/((3k+2)^2)+4/((3k+3)^2)]

(2)
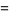= 12sum_(k=0)^(infty)(-1)^k[1/((5k+1)^2)-1/((5k+2)^2)+1/((5k+3)^2)-1/((5k+4)^2)+1/((5k+5)^2)]

(3)
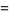= 12sum_(k=0)^(infty)(-1)^k[1/((7k+1)^2)-1/((7k+2)^2)+1/((7k+3)^2)-1/((7k+4)^2)+1/((7k+5)^2)-1/((7k+6)^2)+1/((7k+7)^2)]

(4)
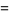= sum_(k=0)^(infty)(-1)^k[(13)/((7k+1)^2)-(13)/((7k+2)^2)+(13)/((7k+3)^2)-(13)/((7k+4)^2)+(13)/((7k+5)^2)-(13)/((7k+6)^2)-(36)/((7k+7)^2)]

(5)
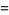= sum_(k=0)^(infty)(-1)^k[(13)/((9k+1)^2)-(13)/((9k+2)^2)+4/((9k+3)^2)-(13)/((9k+4)^2)+(13)/((9k+5)^2)-4/((9k+6)^2)+(13)/((9k+7)^2)-(13)/((9k+8)^2)+4/((9k+9)^2)].

(6)

2^k,

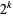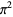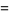pi^2 = sum_(k=0)^(infty)1/(16^k)[8/((8k+1)^2)-8/((8k+2)^2)-4/((8k+3)^2)-8/((8k+4)^2)-2/((8k+5)^2)-2/((8k+6)^2)+1/((8k+7)^2)]

(7)
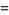= 9/8sum_(k=0)^(infty)1/(64^k)[(16)/((6k+1)^2)-(24)/((6k+2)^2)-8/((6k+3)^2)-6/((6k+4)^2)+1/((6k+5)^2)]

(8)
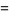= 1/8sum_(k=0)^(infty)1/(256^k)[(128)/((16k+1)^2)-(128)/((16k+2)^2)-(128)/((16k+3)^2)-(128)/((16k+4)^2)-(32)/((16k+5)^2)-(32)/((16k+6)^2)+(16)/((16k+7)^2)+8/((16k+9)^2)-8/((16k+10)^2)-4/((16k+11)^2)-8/((16k+12)^2)-2/((16k+13)^2)-2/((16k+14)^2)+1/((16k+15)^2)]

(9)
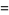= 9/(512)sum_(k=0)^(infty)1/(4096^k)[(1024)/((12k+1)^2)-(1536)/((12k+2)^2)-(512)/((12k+3)^2)-(384)/((12k+4)^2)+(64)/((12k+5)^2)+(16)/((12k+7)^2)-(24)/((12k+8)^2)-8/((12k+9)^2)-6/((12k+10)^2)+1/((12k+11)^2)]

(10)

some of which are noted by Bailey et al. (1997), and 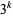3^k,

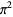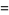pi^2 = 2/(27)sum_(k=0)^(infty)1/(729^k)[(243)/((12k+1)^2)-(405)/((12k+2)^2)-(81)/((12k+4)^2)-(27)/((12k+5)^2)-(72)/((12k+6)^2)-9/((12k+7)^2)-9/((12k+8)^2)-5/((12k+10)^2)+1/((12k+11)^2)]

(11)
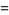= 2sum_(k=0)^(infty)1/(531441^k)[(177147)/((24k+1)^2)-(295245)/((24k+2)^2)-(59049)/((24k+4)^2)-(19683)/((24k+5)^2)-(52488)/((24k+6)^2)-(6561)/((24k+7)^2)-(6561)/((24k+8)^2)-(3645)/((24k+10)^2)+(729)/((24k+11)^2)+(243)/((24k+13)^2)-(405)/((24k+14)^2)-(81)/((24k+16)^2)-(27)/((24k+17)^2)-(72)/((24k+18)^2)-9/((24k+19)^2)-9/((24k+20)^2)-5/((24k+22)^2)+1/((24k+23)^2)].

(12)

Another identity is

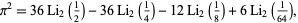pi^2=36Li_2(1/2)-36Li_2(1/4)-12Li_2(1/8)+6Li_2(1/(64)),

(13)

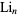where Li_n is the polylogarithm. (13) is equivalent to

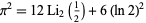pi^2=12Li_2(1/2)+6(ln2)^2

(14)

(Bailey et al. 1997).

REFERENCES:

Bailey, D. H.; Borwein, P.; and Plouffe, S. "On the Rapid Computation of Various Polylogarithmic Constants." Math. Comput. 66, 903-913, 1997.




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
التاريخ / 2024-11-26

الأخبار العلمية
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
التاريخ / 2024-11-26

الساحة الاسلامية
الأمين العام للعتبة العسكرية المقدسة يستقبل شيوخ ووجهاء عشيرة البو بدري في مدينة سامراء
التاريخ / 2024-11-28