

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Pi Digits
المؤلف:
Adamchik, V. and Wagon, S
المصدر:
"A Simple Formula for pi." Amer. Math. Monthly 104
الجزء والصفحة:
...
10-3-2020
3894
Pi Digits
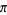 has decimal expansion given by
has decimal expansion given by
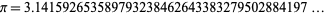 |
(1) |
(OEIS A000796). The following table summarizes some record computations of the digits of 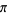 .
.
 |
1999 | Kanada, Ushio and Kuroda |
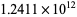 |
Dec. 2002 | Kanada, Ushio and Kuroda (Peterson 2002, Kanada 2003) |
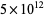 |
Aug. 2012 | A. J. Yee (Yee) |
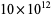 |
Aug. 2012 | S. Kondo and A. J. Yee (Yee) |
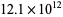 |
Dec. 2013 | A. J. Yee and S. Kondo (Yee) |
The calculation of the digits of 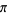 has occupied mathematicians since the day of the Rhind papyrus (1500 BC). Ludolph van Ceulen spent much of his life calculating
has occupied mathematicians since the day of the Rhind papyrus (1500 BC). Ludolph van Ceulen spent much of his life calculating 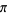 to 35 places. Although he did not live to publish his result, it was inscribed on his gravestone. Wells (1986, p. 48) discusses a number of other calculations. The calculation of
to 35 places. Although he did not live to publish his result, it was inscribed on his gravestone. Wells (1986, p. 48) discusses a number of other calculations. The calculation of 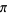 also figures in the Season 2 Star Trek episode "Wolf in the Fold" (1967), in which Captain Kirk and Mr. Spock force an evil entity (composed of pure energy and which feeds on fear) out of the starship Enterprise's computer by commanding the computer to "compute to the last digit the value of pi," thus sending the computer into an infinite loop.
also figures in the Season 2 Star Trek episode "Wolf in the Fold" (1967), in which Captain Kirk and Mr. Spock force an evil entity (composed of pure energy and which feeds on fear) out of the starship Enterprise's computer by commanding the computer to "compute to the last digit the value of pi," thus sending the computer into an infinite loop.
Al-Kāshi of Samarkand computed the sexagesimal digits of 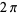 as
as
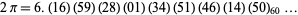 |
(2) |
(OEIS A091649) using 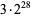 -gons, a value accurate to 17 decimal places (Borwein and Bailey 2003, p. 107).
-gons, a value accurate to 17 decimal places (Borwein and Bailey 2003, p. 107).
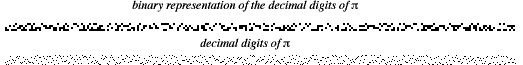
The binary representation of the decimal digits of 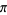 (top figure) and decimal representation (bottom figure) of
(top figure) and decimal representation (bottom figure) of 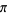 are illustrated above.
are illustrated above.

A plot of the first 1600 decimal digits of 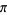 (mod 2) is shown above (left figure), with the corresponding plot for 22/7 shown at right. Here, white indicates an even digit and black an odd digit (Pickover 2002, p. 285).
(mod 2) is shown above (left figure), with the corresponding plot for 22/7 shown at right. Here, white indicates an even digit and black an odd digit (Pickover 2002, p. 285).
Spigot (Rabinowitz and Wagon 1995; Arndt and Haenel 2001; Borwein and Bailey 2003, pp. 140-141) and base-16 digit-extraction algorithms (the BBP formula) are known for 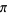 . A remarkable recursive formula conjectured to give the
. A remarkable recursive formula conjectured to give the 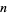 th hexadecimal digit of
th hexadecimal digit of 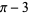 is given by
is given by 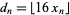 , where
, where 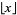 is the floor function,
is the floor function,
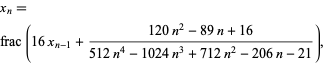 |
(3) |
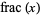 is the fractional part and
is the fractional part and 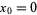 (Borwein and Bailey 2003, Ch. 4; Bailey et al. 2007, pp. 22-23).
(Borwein and Bailey 2003, Ch. 4; Bailey et al. 2007, pp. 22-23).
Pi-primes, i.e., 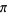 -constant primes occur at 2, 6, 38, 16208, 47577, 78073, 613373, ... (OEIS A060421) decimal digits.
-constant primes occur at 2, 6, 38, 16208, 47577, 78073, 613373, ... (OEIS A060421) decimal digits.
The beast number 666 appears in 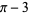 at decimals 2440, 3151, 4000, 4435, 5403, 6840, (OEIS A083625). The first occurrences of just
at decimals 2440, 3151, 4000, 4435, 5403, 6840, (OEIS A083625). The first occurrences of just 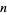 consecutive 6s are 7, 117, 2440, 21880, 48439, 252499, 8209165, 55616210, 45681781, ... (OEIS A096760), while
consecutive 6s are 7, 117, 2440, 21880, 48439, 252499, 8209165, 55616210, 45681781, ... (OEIS A096760), while 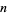 (or more) consecutive 6s first occur at 7, 117, 2440, 21880, 48439, 252499, 8209165, 45681781, 45681781, ... (OEIS A050285).
(or more) consecutive 6s first occur at 7, 117, 2440, 21880, 48439, 252499, 8209165, 45681781, 45681781, ... (OEIS A050285).
The digits 314159 appear at positions 176451, 1259351, 1761051, 6467324, 6518294, 9753731, 9973760, ... (correcting Pickover 1995).
The sequence 0123456789 occurs beginning at digits 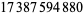 ,
, 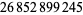 ,
, 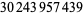 ,
, 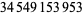 ,
, 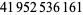 , and
, and 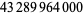 (OEIS A101815; cf. Wells 1986, pp. 51-52).
(OEIS A101815; cf. Wells 1986, pp. 51-52).
The sequence 9876543210 occurs beginning at digits 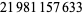 ,
, 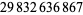 ,
, 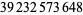 ,
, 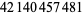 , and
, and 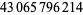 (OEIS A101816).
(OEIS A101816).
The sequence 27182818284 (the first few digits of e) occurs beginning at digit 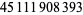 (see also Pickover's sequence).
(see also Pickover's sequence).
There are also interesting patterns for 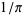 . 0123456789 occurs at
. 0123456789 occurs at 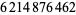 , 9876543210 occurs at
, 9876543210 occurs at 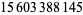 and
and 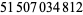 , and 999999999999 occurs at
, and 999999999999 occurs at 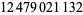 of
of 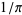 .
.
The starting positions of the first occurrence of 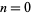 , 1, 2, ... in the decimal expansion of
, 1, 2, ... in the decimal expansion of 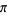 (including the initial 3 and counting it as the first digit) are 33, 2, 7, 1, 3, 5, 8, 14, ... (OEIS A032445).
(including the initial 3 and counting it as the first digit) are 33, 2, 7, 1, 3, 5, 8, 14, ... (OEIS A032445).
Scanning the decimal expansion of 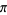 until all
until all 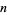 -digit numbers have occurred, the last 1-, 2-, ... digit numbers appearing are 0, 68, 483, 6716, 33394, 569540, ... (OEIS A032510), which end at digits 33, 607, 8556, 99850, 1369565, ... (OEIS A080597).
-digit numbers have occurred, the last 1-, 2-, ... digit numbers appearing are 0, 68, 483, 6716, 33394, 569540, ... (OEIS A032510), which end at digits 33, 607, 8556, 99850, 1369565, ... (OEIS A080597).
A curiosity relating 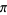 to the beast number 666 involves adding the first three sextads of
to the beast number 666 involves adding the first three sextads of 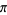 . First, note that
. First, note that
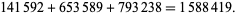 |
(4) |
Now, skip ahead 15 decimal places and note that the sum is repeated as
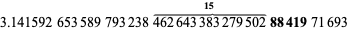 |
(5) |
(pers. comm., P. Olivera, Aug. 11, 2005; Olivera).
It is not known if 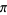 is normal (Wagon 1985, Bailey and Crandall 2001), although the first 30 million digits are very uniformly distributed (Bailey 1988).
is normal (Wagon 1985, Bailey and Crandall 2001), although the first 30 million digits are very uniformly distributed (Bailey 1988).
The following distribution of decimal digits 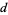 is found for the first
is found for the first 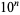 digits of
digits of 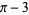 (Kanada 2003). It shows no statistically significant departure from a uniform distribution.
(Kanada 2003). It shows no statistically significant departure from a uniform distribution.
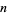 |
OEIS | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 0 | A099291 | 8 | 93 | 968 | 9999 | 99959 | 999440 | 9999922 | 99993942 | 999967995 | 10000104750 | 99999485134 |
| 1 | A099292 | 8 | 116 | 1026 | 10137 | 99758 | 999333 | 10002475 | 99997334 | 1000037790 | 9999937631 | 99999945664 |
| 2 | A099293 | 12 | 103 | 1021 | 9908 | 100026 | 1000306 | 10001092 | 100002410 | 1000017271 | 10000026432 | 100000480057 |
| 3 | A099294 | 11 | 102 | 974 | 10025 | 100229 | 999964 | 9998442 | 99986911 | 999976483 | 9999912396 | 99999787805 |
| 4 | A099295 | 10 | 93 | 1012 | 9971 | 100230 | 1001093 | 10003863 | 100011958 | 999937688 | 10000032702 | 100000357857 |
| 5 | A099296 | 8 | 97 | 1046 | 10026 | 100359 | 1000466 | 9993478 | 99998885 | 1000007928 | 9999963661 | 99999671008 |
| 6 | A099297 | 9 | 94 | 1021 | 10029 | 99548 | 999337 | 9999417 | 100010387 | 999985731 | 9999824088 | 99999807503 |
| 7 | A099298 | 8 | 95 | 970 | 10025 | 99800 | 1000207 | 9999610 | 99996061 | 1000041330 | 10000084530 | 99999818723 |
| 8 | A099299 | 12 | 101 | 948 | 9978 | 99985 | 999814 | 10002180 | 100001839 | 999991772 | 10000157175 | 100000791469 |
| 9 | A099300 | 14 | 106 | 1014 | 9902 | 100106 | 1000040 | 9999521 | 100000273 | 1000036012 | 9999956635 | 99999854780 |
The following table gives the first few positions at which a digit 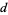 occurs
occurs 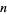 times. The sequence 1, 135, 1698, 54525, 24466, 252499, 3346228, 46663520, 564665206, ... (OEIS A061073) given by the diagonal (plus any terms of the form 10 10's etc.) is known as the Earls sequence (Pickover 2002, p. 339). The sequence 999999 occurs at decimal 762 (which is sometimes called the Feynman point; Wells 1986, p. 51) and continues as 9999998, which is largest value of any seven digits in the first million decimals.
times. The sequence 1, 135, 1698, 54525, 24466, 252499, 3346228, 46663520, 564665206, ... (OEIS A061073) given by the diagonal (plus any terms of the form 10 10's etc.) is known as the Earls sequence (Pickover 2002, p. 339). The sequence 999999 occurs at decimal 762 (which is sometimes called the Feynman point; Wells 1986, p. 51) and continues as 9999998, which is largest value of any seven digits in the first million decimals.
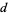 |
OEIS | strings of 1, 2, ...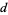 s first occur at s first occur at |
| 0 | A050279 | 32, 307, 601, 13390, 17534, 1699927, ... |
| 1 | A035117 | 1, 94, 153, 12700, 32788, 255945, ... |
| 2 | A050281 | 6, 135, 1735, 4902, 65260, 963024, ... |
| 3 | A050282 | 9, 24, 1698, 28467, 28467, 710100, ... |
| 4 | A050283 | 2, 59, 2707, 54525, 808650, 828499, ... |
| 5 | A050284 | 4, 130, 177, 24466, 24466, 244453, ... |
| 6 | A050285 | 7, 117, 2440, 21880, 48439, 252499, ... |
| 7 | A050286 | 13, 559, 1589, 1589, 162248, 399579, ... |
| 8 | A050287 | 11, 34, 4751, 4751, 213245, 222299, ... |
| 9 | A048940 | 5, 44, 762, 762, 762, 762, 1722776, ... |
REFERENCES:
Adamchik, V. and Wagon, S. "A Simple Formula for 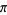 ." Amer. Math. Monthly 104, 852-855, 1997.
." Amer. Math. Monthly 104, 852-855, 1997.
Anderson, D. "The Pi-Search Page." http://www.angio.net/pi/piquery.
Arndt, J. and Haenel, C. Pi--Unleashed, 2nd ed. Berlin: Springer-Verlag, 2001.
Bailey, D. H. "The Computation of 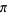 to
to 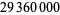 Decimal Digit using Borwein's' Quartically Convergent Algorithm." Math. Comput. 50, 283-296, 1988.
Decimal Digit using Borwein's' Quartically Convergent Algorithm." Math. Comput. 50, 283-296, 1988.
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007.
Bailey, D. H.; Borwein, P. B.; and Plouffe, S. "On the Rapid Computation of Various Polylogarithmic Constants." Math. Comput. 66, 903-913, 1997.
Bailey, D. H. and Crandall, R. E. "On the Random Character of Fundamental Constant Expansions." Exper. Math. 10, 175-190, 2001. http://www.nersc.gov/~dhbailey/dhbpapers/baicran.pdf.
Borwein, J. M. "Talking About Pi." http://www.cecm.sfu.ca/personal/jborwein/pi_cover.html.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Borwein, J. M.; Borwein, P. B.; and Bailey, D. H. "Ramanujan, Modular Equations, and Approximations to Pi, or How to Compute One Billion Digits of Pi." Amer. Math. Monthly 96, 201-219, 1989.
Caldwell, C. K. and Dubner, H. "Primes in Pi." J. Recr. Math. 29, 282-289, 1998.
Gibbs, W. W. "A Digital Slice of Pi. The New Way to do Pure Math: Experimentally." Sci. Amer. 288, 23-24, May 2003.
Gourdon, X. and Sebah, P. "PiFast: The Fastest Program to Compute Pi." http://numbers.computation.free.fr/Constants/PiProgram/pifast.html.
Kanada, Y. "New World Record of Pi: 51.5 Billion Decimal Digits." http://www.cecm.sfu.ca/personal/jborwein/Kanada_50b.html.
Kanada, Y. "Our Latest Record." Sep. 20, 1999. ftp://www.cc.u-tokyo.ac.jp/README.our_latest_record
Kanada, Y. "Sample Digits for Decimal Digits of Pi." Jan. 18, 2003. http://www.super-computing.org/pi-decimal_current.html.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, pp. 22 and 50, 1983.
National Energy Research Scientific Computing Center. "Search 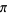 ." http://pi.nersc.gov/.
." http://pi.nersc.gov/.
Olivera, P. "brief Description of Events About How I Found a Curious Pattern in Pi, Many Years Ago, While Searching for Patterns and Sequences." http://www.geocities.com/pi_curiosity/englishstory.html.
Peterson, I. "Pick a Digit, Any Digit." Sci. News Online, Feb. 28, 1998. http://www.sciencenews.org/sn_arc98/2_28_98/mathland.htm.
Peterson, I. "Pi by the Billions." Sci. News 156, 255, Oct. 16, 1999.
Peterson, I. "Pi à la mode." Sci. News 160, 136-137, Sep. 1, 2001. http://www.sciencenews.org/20010901/bob9.asp.
Peterson, I. "A Passion for Pi." In Mathematical Treks: From Surreal Numbers to Magic Circles. Washington, DC: Math. Assoc. Amer., 2001.
Peterson, I. "MathTrek: A Trillion Pieces of Pi." Dec. 14, 2002. http://www.sciencenews.org/20021214/mathtrek.asp.
Pickover, C. A. Keys to Infinity. New York: Wiley, p. 62, 1995.
Pickover, C. A. The Mathematics of Oz: Mental Gymnastics from Beyond the Edge. New York: Cambridge University Press, pp. 284-285, 2002.
Plouffe, S. "Table of Current Records for the Computation of Constants." http://pi.lacim.uqam.ca/eng/records_en.html.
Rabinowitz, S. and Wagon, S. "A Spigot Algorithm for the Digits of 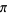 ." Amer. Math. Monthly 102, 195-203, 1995.
." Amer. Math. Monthly 102, 195-203, 1995.
Sloane, N. J. A. Sequences A000796/M2218, A032150, A032445, A035117, A036903, A036974, A037000, A037001, A037002, A037003, A037004, A037005, A037006, A037007, A037008, A048940, A050201, A050202, A050203, A050208, A050209, A050215, A050222, A050230, A050238, A050245, A050254, A050263, A050272, A050279, A050281, A050282, A050283, A050284, A050285, A050286, A050287, A060421, A061073, A080597, A083625, A091649, A096760, A099291, A099292, A099293, A099294, A099295, A099296, A099297, A099298, A099299, A099300, A101815, and A101816 in "The On-Line Encyclopedia of Integer Sequences."
Smith, H. J. "Computing Pi." http://www.geocities.com/hjsmithh/Pi.html.
Wagon, S. "Is 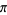 Normal?" Math. Intel. 7, 65-67, 1985.
Normal?" Math. Intel. 7, 65-67, 1985.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 46, 1986.
Wrench, J. W. Jr. "The Evolution of Extended Decimal Approximations to 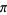 ." Math. Teacher 53, 644-650, 1960.
." Math. Teacher 53, 644-650, 1960.
Yee, A. J. "y-cruncher - A Multi-Threaded Pi-Program." http://www.numberworld.org/y-cruncher/.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















